Please follow the instruction(ONLY IN JAVA)

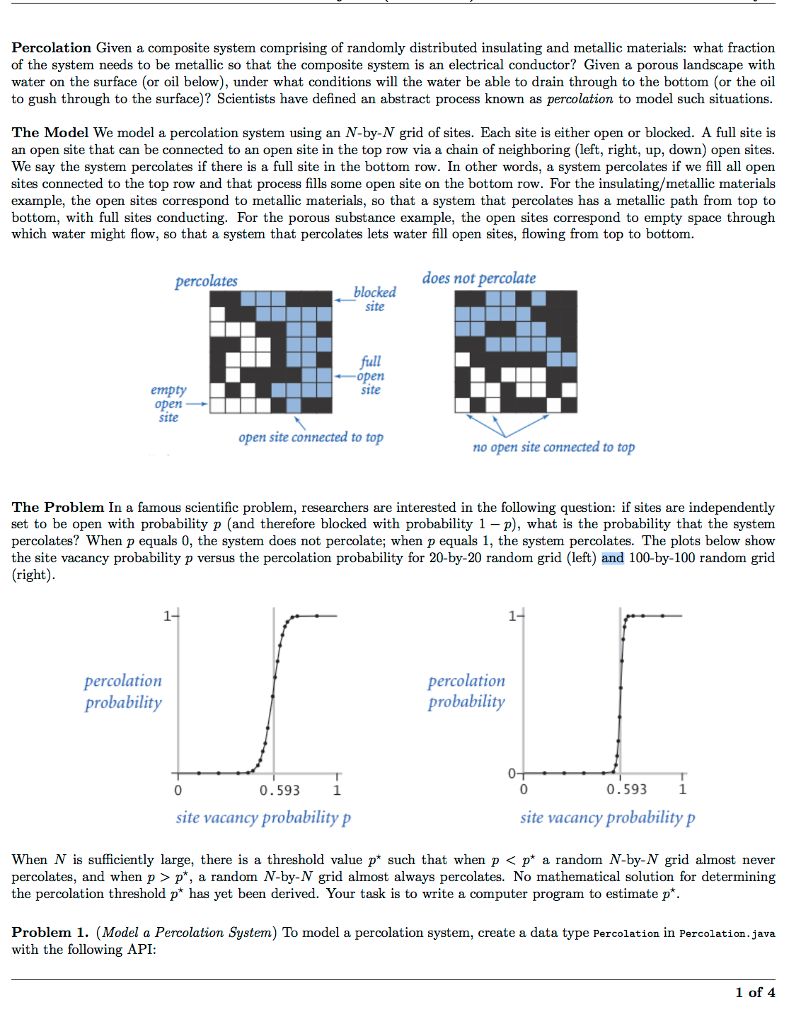
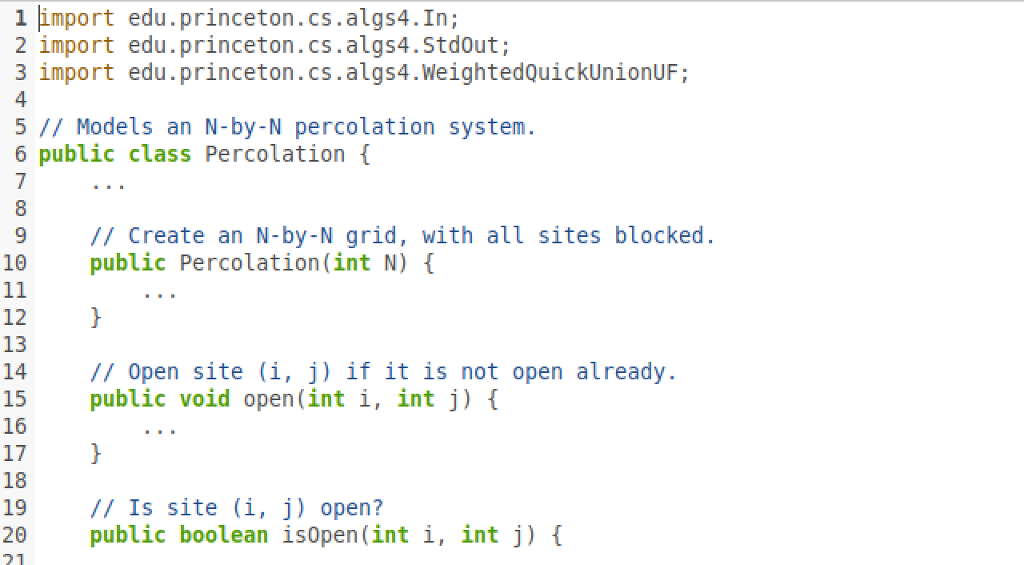
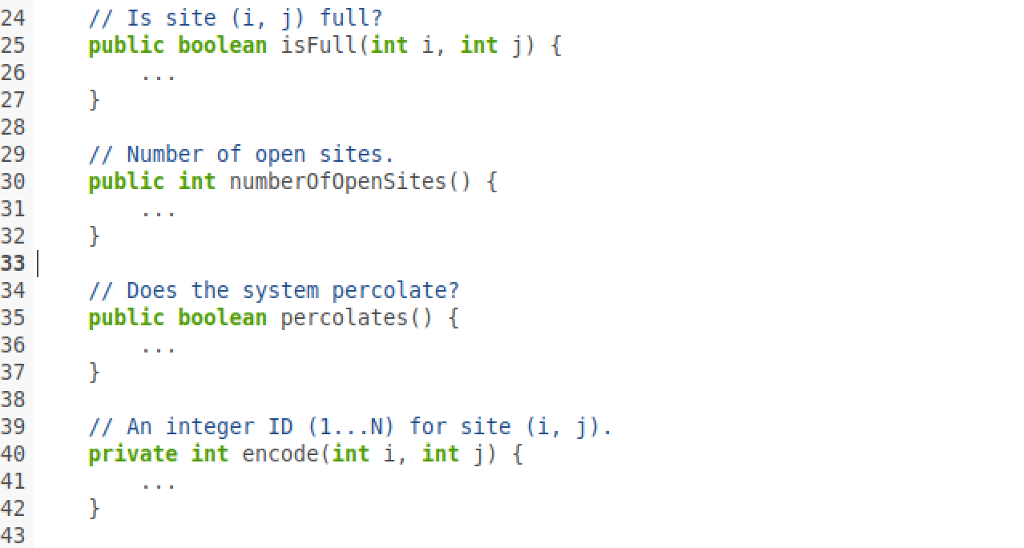
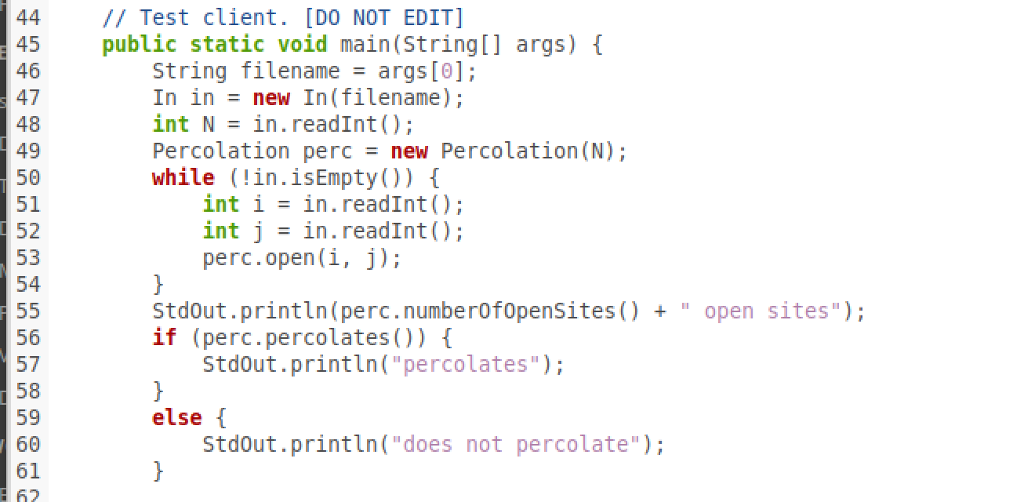
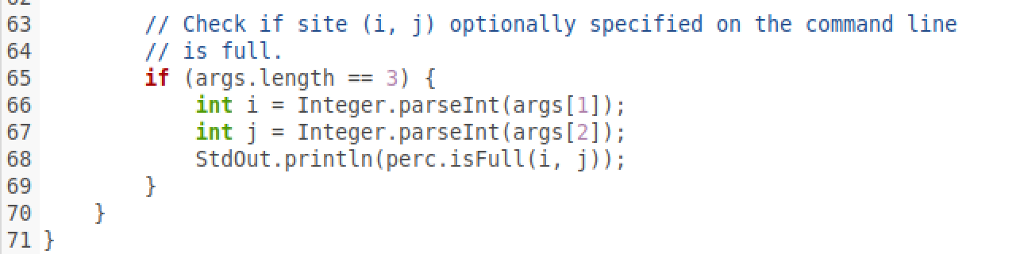
Percolation Given a composite system comprising of randomly distributed insulating and metallic materials: what fraction of the system needs to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations The Model We model a percolation system using an N-by-N grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom. blocked does not percolate site full open site empty open open site connected to top no open site connected to top The Problem In a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and therefore blocked with probability 1-p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20-by-20 random grid (left) and 100-by-100 random grid (right) 1 1 percolation probability percolationm probability 0.593 1 0.5931 site vacancy probability p site vacancy probability p When N is sufficiently large, there is a threshold value p* such that when p p*, a random N-by-N grid almost always percolates. No mathematical solution for determining the percolation threshold p* has yet been derived. Your task is to write a computer program to estimate p. Problem 1. (Model a Percolation System) To model a percolation system, create a data type Percolation in Percolation.java with the following API 1 of 4 Percolation Given a composite system comprising of randomly distributed insulating and metallic materials: what fraction of the system needs to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations The Model We model a percolation system using an N-by-N grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom. blocked does not percolate site full open site empty open open site connected to top no open site connected to top The Problem In a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and therefore blocked with probability 1-p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20-by-20 random grid (left) and 100-by-100 random grid (right) 1 1 percolation probability percolationm probability 0.593 1 0.5931 site vacancy probability p site vacancy probability p When N is sufficiently large, there is a threshold value p* such that when p p*, a random N-by-N grid almost always percolates. No mathematical solution for determining the percolation threshold p* has yet been derived. Your task is to write a computer program to estimate p. Problem 1. (Model a Percolation System) To model a percolation system, create a data type Percolation in Percolation.java with the following API 1 of 4