Question: please help!! . Aa. 21 AaBbcd AaBbcc AaBbc AaBbcc Aa Normal T No Spac... Heading 1 Heading 2 Tit Paragraph Styles 5 6 A real
please help!! . 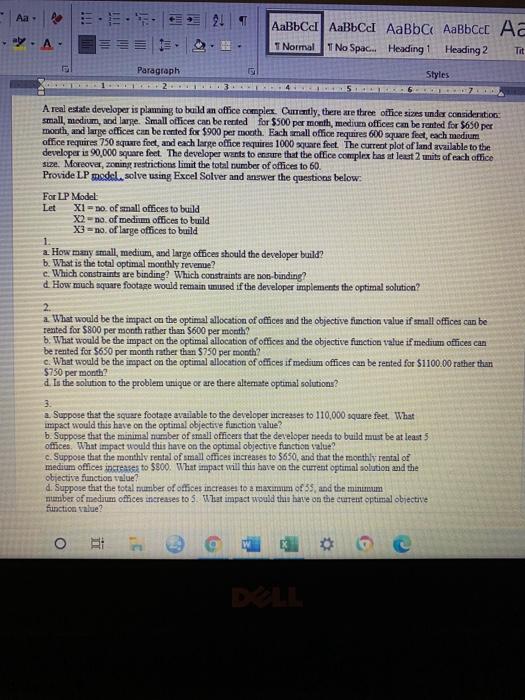

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


