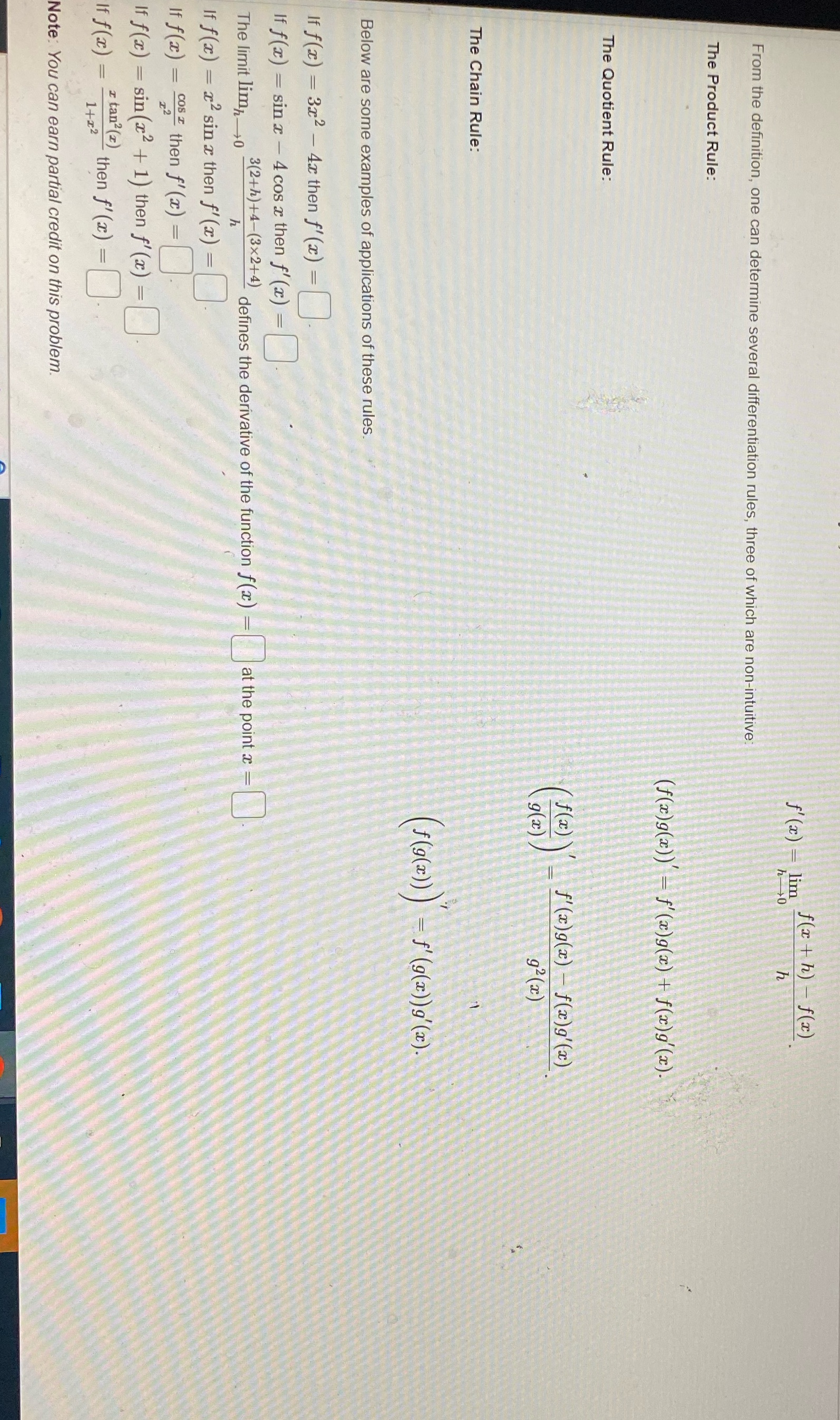
Question: Please help f' (a) - lim f ( I t h) - f(x) From the definition, one can determine several differentiation rules, three of which
Please help
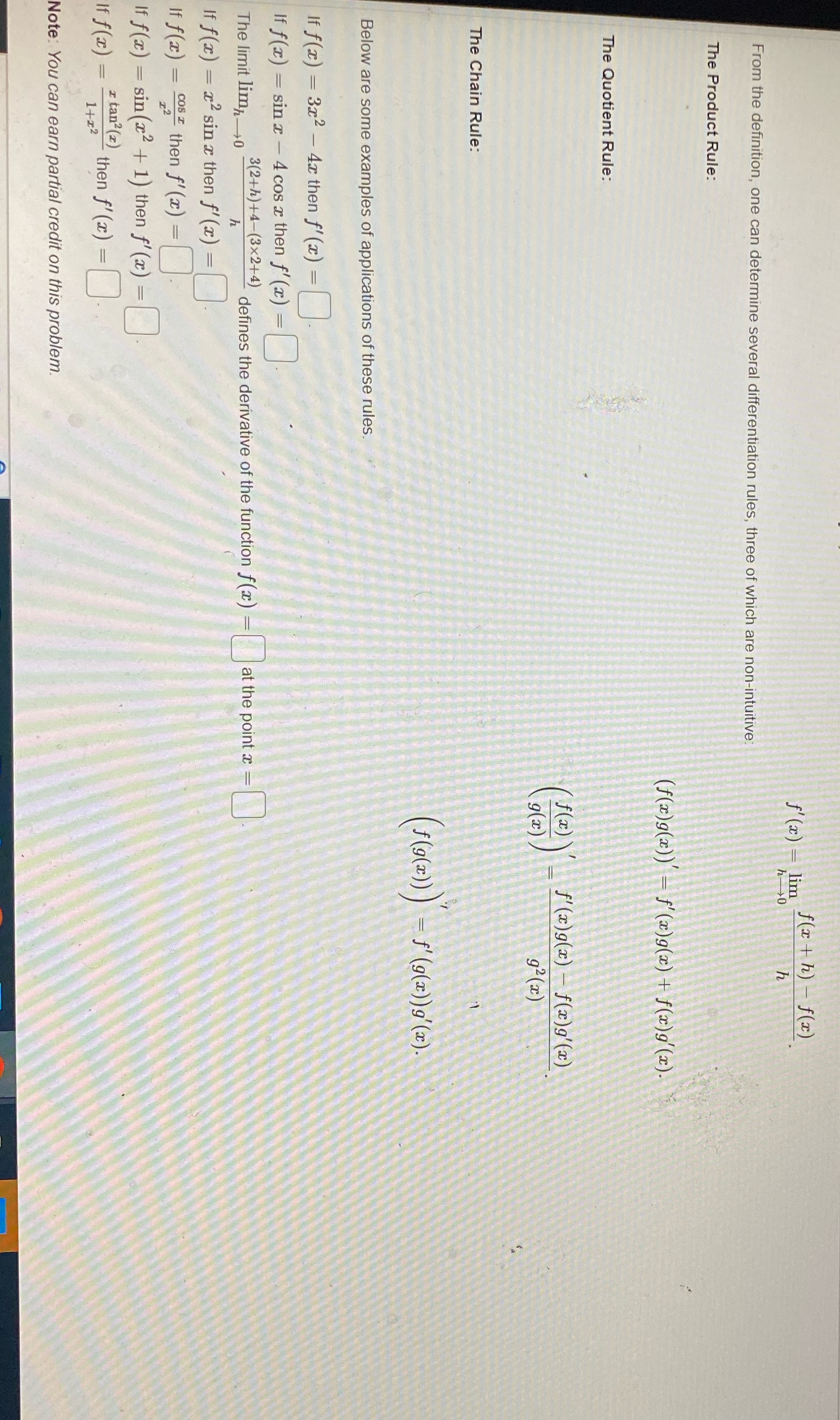
f' (a) - lim f ( I t h) - f(x) From the definition, one can determine several differentiation rules, three of which are non-intuitive: The Product Rule: (f ( ze) 9 (20 ) ) ' - f'(2.) 9(x) + f(2)9'(2). The Quotient Rule: (f (z) 'f'(x)g(x) -f(x)9'(2) g (2 ) 92 (x) The Chain Rule: (F (9 ( z ) ) ) - S' ( 9 ( 2 ) ) 9 ' ( 2 ) . Below are some examples of applications of these rules. If f(I) = 3x2 - 4x then f'(2) = If f(x) = sin x - 4 cos a then f'(x) = The limit limp-+0 3 ( 2 + h ) + 4 - ( 3 x 2 + 4 ) defines the derivative of the function f(a) = at the point x - If f(a) = 2 sin a then f' (x) = If f (at ) = cos I then f'(at) = If f() = sin(x2+ 1) then f' (ze) = If f ( ac ) = 1+ 2 2 I tan.(2) then f' (z) = Note: You can earn partial credit on this
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


