PLEASE help me answer these problems. Please do not attempt to answer unless you can help me answer ALL questions! please show work as this is needed for studying! thank you in advance, will rate :)

sorry it uploaded sideways but here it is and pg 383

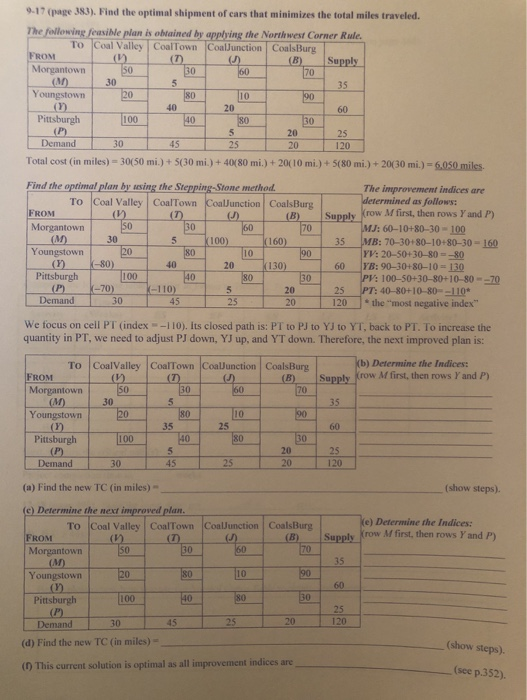
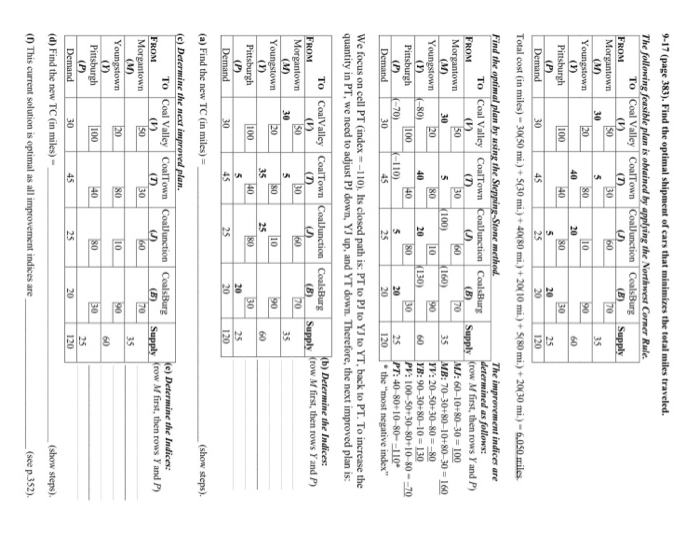
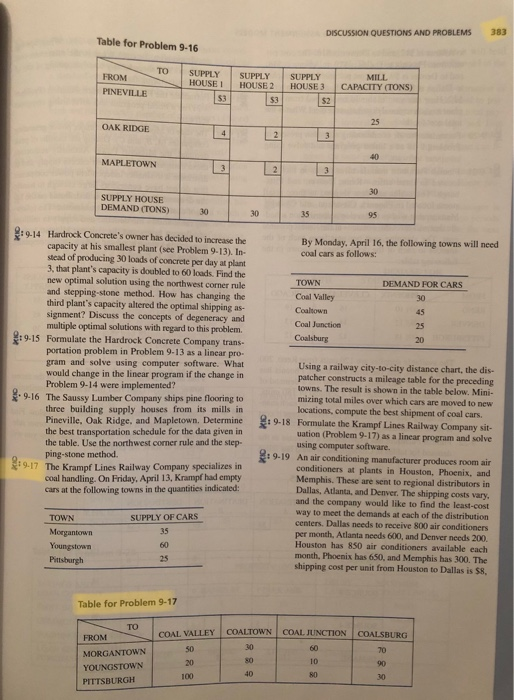
9-17 (page 383). Find the optimal shipment of cars that minimizes the total miles traveled. The following feasible plan is obtained by applying the Northwest Corner Rule. To Coal Valley CoalTown CoalJunction CoalsBurg FROM (U) (B) Supply Morgantown 50 30 70 30 Youngstown 20 (1) 40 Pittsburgh 100 Demand 45 Total cost (in miles) - 30450 mi.) 5(30 mi.) + 40(80 mi.) + 2010 m.) +5(80 mi) + 20(30 mi.) -6.050 miles Supply Find the optimal plan by using the Stepping-Stone method. To Coal Valley Coal Town CoalJunction CoalsBurg FROM (1) (1) () (B) Morgantown 50 30 60 5 k100) 160) Youngstown 20 (1) -80) Pittsburgh ( 70) 110) Demand 30 The improvement indices are determined as follows: row M first, then rows Yand P) MJ: 60-10+80-30 = 100 MB: 70-30+80-10+80-30 = 160 YV: 20-50-30-80 = -80 YB: 90-30-80-10= 130 PV: 100-50+30-80+10 80 - -70 PT: 40 8010 80-110 t he "most negative index" 130) 25 120 We focus on cell PT (index=-110). Its closed path is: PT to PJ to YJ to YT, back to PT. To increase the quantity in PT, we need to adjust PJ down, YJ up, and YT down. Therefore, the next improved plan is: To Coal Valley CoalTown Coal Junction CoalsBurg FROM UB Morgantown 50 30 (b) Determine the Indices: Supply row Mfirst, then rows Y and P) Youngstown 20 SO 10 Pittsburgh 100 NO 30 40 45 Demand 2520 (a) Find the new TC (in miles) = (show steps) (c) Determine the next improved plan. To Coal Valley CoalTown FROM + (0 Morgantown 50 Coaldunction () CoalsBurg (B) 70 e ) Determine the Indices Supply Krow first, then rows Yand P) 35 Youngstown 20 80 Pittsburgh 100 40 80 25 45 2 5 20 120 Demand 30 (d) Find the new TC (in miles) - (show steps) (1) This current solution is optimal as all improvement indices are (see p.352). 70 0.17 (page 383). Find the optimal shipment of cars that minimizes the total miles traveled. The following feasile plan is obtained by applying the Northwest Corner Rule. To Coal Valley Coal Town CoalJunction CoalsBurg FROM (1) (7) (B) Supply Morgantown 5 0 30 60 (M) 305 Youngstown 20 80 10 90 ( 1 20 60 Pittsburgh 100 80 5 20 25 Demand 30 45 20 Total cost (in miles) = 30(50 mi.) +(30 mi.) + 40(80 mi.) +2010 m.) +5(80 mi.) +20(30 mi.) - 6,050 miles Ae 30 P 25 120 Find the optimal plan by using the Stepping-Stone method. To Coal Valley Coal Town CoalJunction CoalsBurg FROM (0 ) (B) Morgantown S0 3 0 30 5 100) (160) Youngstown 20 8 0 10 90 (1) K-80) 40 2 0 130) Pittsburgh 100 40 80 30 (P) -70) -110) 5 20 Demand 30 45 25 20 The improvement indices are determined as follows: Supply Krow Mfirst, then rows and P) MJ: 60-10+80-30-100 35 MB: 70-30+80-10+80-30 - 160 YV: 20-50+30-80 = -80 60 YB: 90-30+80-10 = 130 PV: 100-50+30-80+10-80 -70 25 PT: 40-80+10-80-110* 120 the most negative index" We focus on cell PT (index = -110). Its closed path is: PT to PJ to YJ to YT, back to PT. To increase the quantity in PT, we need to adjust PJ down, YJ up, and YT down. Therefore, the next improved plan is: CoalsBurg (B) kb) Determine the Indices: Supply Krow M first, then rows Y and P) To CoalValley Coal Town Coaldunction FROM (1) ( DJ) Morgantown 50 30 60 30 Youngstown (2 Pittsburgh Demand 30 45 25 20 (a) Find the new TC (in miles) - (show steps). Ke) Determine the Indices: Supply Krow M first, then rows Y and P) (e) Determine the next improved plan. To Coal Valley Coal Town CoalJunction CoalsBurg FROM Morgantown (M ) Youngstown 20 80 Pittsburgh 100 40 80 30 (P) Demand 30 45 25 (d) Find the new TC (in miles) - (1) This current solution is optimal as all improvement indices are (show steps). (see p.352) DISCUSSION QUESTIONS AND PROBLEMS 383 Table for Problem 9-16 TO FROM PINEVILLE SUPPLY HOUSE SUPPLY HOUSE 2 SUPPLY HOUSE 3 MILL CAPACITY (TONS) OAK RIDGE MAPLETOWN SUPPLY HOUSE DEMAND (TONS) 30 35 By Monday, April 16, the following towns will need coal cars as follows: TOWN DEMAND FOR CARS Coal Valley Coaltown Coal Junction Coalsburg 2:9-14 Hardrock Concrete's owner has decided to increase the capacity at his smallest plant (see Problem 9-13). In- stead of producing 30 loads of concrete per day at plant 3. that plant's capacity is doubled to 60 loads. Find the new optimal solution using the northwest corner rule and stepping-stone method. How has changing the third plant's capacity altered the optimal shipping as- signment? Discuss the concepts of degeneracy and multiple optimal solutions with regard to this problem. :9-15 Formulate the Hardrock Concrete Company trans- portation problem in Problem 9-13 as a linear pro- gram and solve using computer software. What would change in the linear program if the change in Problem 9-14 were implemented? 9-16 The Saussy Lumber Company ships pine flooring to three building supply houses from its mills in Pineville, Oak Ridge, and Mapletown. Determine the best transportation schedule for the data given in the table. Use the northwest corner rule and the step- ping-stone method 19.17 The Krampf Lines Railway Company specializes in coal handling. On Friday, April 13, Krampf had empty cars at the following towns in the quantities indicated: Using a railway city-to-city distance chart, the dis- patcher constructs a mileage table for the preceding towns. The result is shown in the table below. Mini- mizing total miles over which cars are moved to new locations, compute the best shipment of coal cars. P: 9-18 Formulate the Krampf Lines Railway Company sit- uation (Problem 9-17) as a linear program and solve using computer software. 19-19 An air conditioning manufacturer produces room air conditioners at plants in Houston, Phoenix, and Memphis. These are sent to regional distributors in Dallas, Atlanta, and Denver. The shipping costs vary. and the company would like to find the least-cost way to meet the demands at each of the distribution centers. Dallas needs to receive 800 air conditioners per month, Atlanta needs 600, and Denver needs 200. Houston has 850 air conditioners available each month, Phoenix has 650, and Memphis has 300. The shipping cost per unit from Houston to Dallas is $8. TOWN SUPPLY OF CARS Morgantown Youngstown Pittsburgh Table for Problem 9-17 TO COAL VALLEY COALTOWN COAL JUNCTION FROM COALSBURG MORGANTOWN YOUNGSTOWN PITTSBURGH 20 100 40 9-17 (page 383). Find the optimal shipment of cars that minimizes the total miles traveled. The following feasible plan is obtained by applying the Northwest Corner Rule. To Coal Valley CoalTown CoalJunction CoalsBurg FROM (U) (B) Supply Morgantown 50 30 70 30 Youngstown 20 (1) 40 Pittsburgh 100 Demand 45 Total cost (in miles) - 30450 mi.) 5(30 mi.) + 40(80 mi.) + 2010 m.) +5(80 mi) + 20(30 mi.) -6.050 miles Supply Find the optimal plan by using the Stepping-Stone method. To Coal Valley Coal Town CoalJunction CoalsBurg FROM (1) (1) () (B) Morgantown 50 30 60 5 k100) 160) Youngstown 20 (1) -80) Pittsburgh ( 70) 110) Demand 30 The improvement indices are determined as follows: row M first, then rows Yand P) MJ: 60-10+80-30 = 100 MB: 70-30+80-10+80-30 = 160 YV: 20-50-30-80 = -80 YB: 90-30-80-10= 130 PV: 100-50+30-80+10 80 - -70 PT: 40 8010 80-110 t he "most negative index" 130) 25 120 We focus on cell PT (index=-110). Its closed path is: PT to PJ to YJ to YT, back to PT. To increase the quantity in PT, we need to adjust PJ down, YJ up, and YT down. Therefore, the next improved plan is: To Coal Valley CoalTown Coal Junction CoalsBurg FROM UB Morgantown 50 30 (b) Determine the Indices: Supply row Mfirst, then rows Y and P) Youngstown 20 SO 10 Pittsburgh 100 NO 30 40 45 Demand 2520 (a) Find the new TC (in miles) = (show steps) (c) Determine the next improved plan. To Coal Valley CoalTown FROM + (0 Morgantown 50 Coaldunction () CoalsBurg (B) 70 e ) Determine the Indices Supply Krow first, then rows Yand P) 35 Youngstown 20 80 Pittsburgh 100 40 80 25 45 2 5 20 120 Demand 30 (d) Find the new TC (in miles) - (show steps) (1) This current solution is optimal as all improvement indices are (see p.352). 70 0.17 (page 383). Find the optimal shipment of cars that minimizes the total miles traveled. The following feasile plan is obtained by applying the Northwest Corner Rule. To Coal Valley Coal Town CoalJunction CoalsBurg FROM (1) (7) (B) Supply Morgantown 5 0 30 60 (M) 305 Youngstown 20 80 10 90 ( 1 20 60 Pittsburgh 100 80 5 20 25 Demand 30 45 20 Total cost (in miles) = 30(50 mi.) +(30 mi.) + 40(80 mi.) +2010 m.) +5(80 mi.) +20(30 mi.) - 6,050 miles Ae 30 P 25 120 Find the optimal plan by using the Stepping-Stone method. To Coal Valley Coal Town CoalJunction CoalsBurg FROM (0 ) (B) Morgantown S0 3 0 30 5 100) (160) Youngstown 20 8 0 10 90 (1) K-80) 40 2 0 130) Pittsburgh 100 40 80 30 (P) -70) -110) 5 20 Demand 30 45 25 20 The improvement indices are determined as follows: Supply Krow Mfirst, then rows and P) MJ: 60-10+80-30-100 35 MB: 70-30+80-10+80-30 - 160 YV: 20-50+30-80 = -80 60 YB: 90-30+80-10 = 130 PV: 100-50+30-80+10-80 -70 25 PT: 40-80+10-80-110* 120 the most negative index" We focus on cell PT (index = -110). Its closed path is: PT to PJ to YJ to YT, back to PT. To increase the quantity in PT, we need to adjust PJ down, YJ up, and YT down. Therefore, the next improved plan is: CoalsBurg (B) kb) Determine the Indices: Supply Krow M first, then rows Y and P) To CoalValley Coal Town Coaldunction FROM (1) ( DJ) Morgantown 50 30 60 30 Youngstown (2 Pittsburgh Demand 30 45 25 20 (a) Find the new TC (in miles) - (show steps). Ke) Determine the Indices: Supply Krow M first, then rows Y and P) (e) Determine the next improved plan. To Coal Valley Coal Town CoalJunction CoalsBurg FROM Morgantown (M ) Youngstown 20 80 Pittsburgh 100 40 80 30 (P) Demand 30 45 25 (d) Find the new TC (in miles) - (1) This current solution is optimal as all improvement indices are (show steps). (see p.352) DISCUSSION QUESTIONS AND PROBLEMS 383 Table for Problem 9-16 TO FROM PINEVILLE SUPPLY HOUSE SUPPLY HOUSE 2 SUPPLY HOUSE 3 MILL CAPACITY (TONS) OAK RIDGE MAPLETOWN SUPPLY HOUSE DEMAND (TONS) 30 35 By Monday, April 16, the following towns will need coal cars as follows: TOWN DEMAND FOR CARS Coal Valley Coaltown Coal Junction Coalsburg 2:9-14 Hardrock Concrete's owner has decided to increase the capacity at his smallest plant (see Problem 9-13). In- stead of producing 30 loads of concrete per day at plant 3. that plant's capacity is doubled to 60 loads. Find the new optimal solution using the northwest corner rule and stepping-stone method. How has changing the third plant's capacity altered the optimal shipping as- signment? Discuss the concepts of degeneracy and multiple optimal solutions with regard to this problem. :9-15 Formulate the Hardrock Concrete Company trans- portation problem in Problem 9-13 as a linear pro- gram and solve using computer software. What would change in the linear program if the change in Problem 9-14 were implemented? 9-16 The Saussy Lumber Company ships pine flooring to three building supply houses from its mills in Pineville, Oak Ridge, and Mapletown. Determine the best transportation schedule for the data given in the table. Use the northwest corner rule and the step- ping-stone method 19.17 The Krampf Lines Railway Company specializes in coal handling. On Friday, April 13, Krampf had empty cars at the following towns in the quantities indicated: Using a railway city-to-city distance chart, the dis- patcher constructs a mileage table for the preceding towns. The result is shown in the table below. Mini- mizing total miles over which cars are moved to new locations, compute the best shipment of coal cars. P: 9-18 Formulate the Krampf Lines Railway Company sit- uation (Problem 9-17) as a linear program and solve using computer software. 19-19 An air conditioning manufacturer produces room air conditioners at plants in Houston, Phoenix, and Memphis. These are sent to regional distributors in Dallas, Atlanta, and Denver. The shipping costs vary. and the company would like to find the least-cost way to meet the demands at each of the distribution centers. Dallas needs to receive 800 air conditioners per month, Atlanta needs 600, and Denver needs 200. Houston has 850 air conditioners available each month, Phoenix has 650, and Memphis has 300. The shipping cost per unit from Houston to Dallas is $8. TOWN SUPPLY OF CARS Morgantown Youngstown Pittsburgh Table for Problem 9-17 TO COAL VALLEY COALTOWN COAL JUNCTION FROM COALSBURG MORGANTOWN YOUNGSTOWN PITTSBURGH 20 100 40