Please help me answer this. Kindly show your solutions. Thank you!

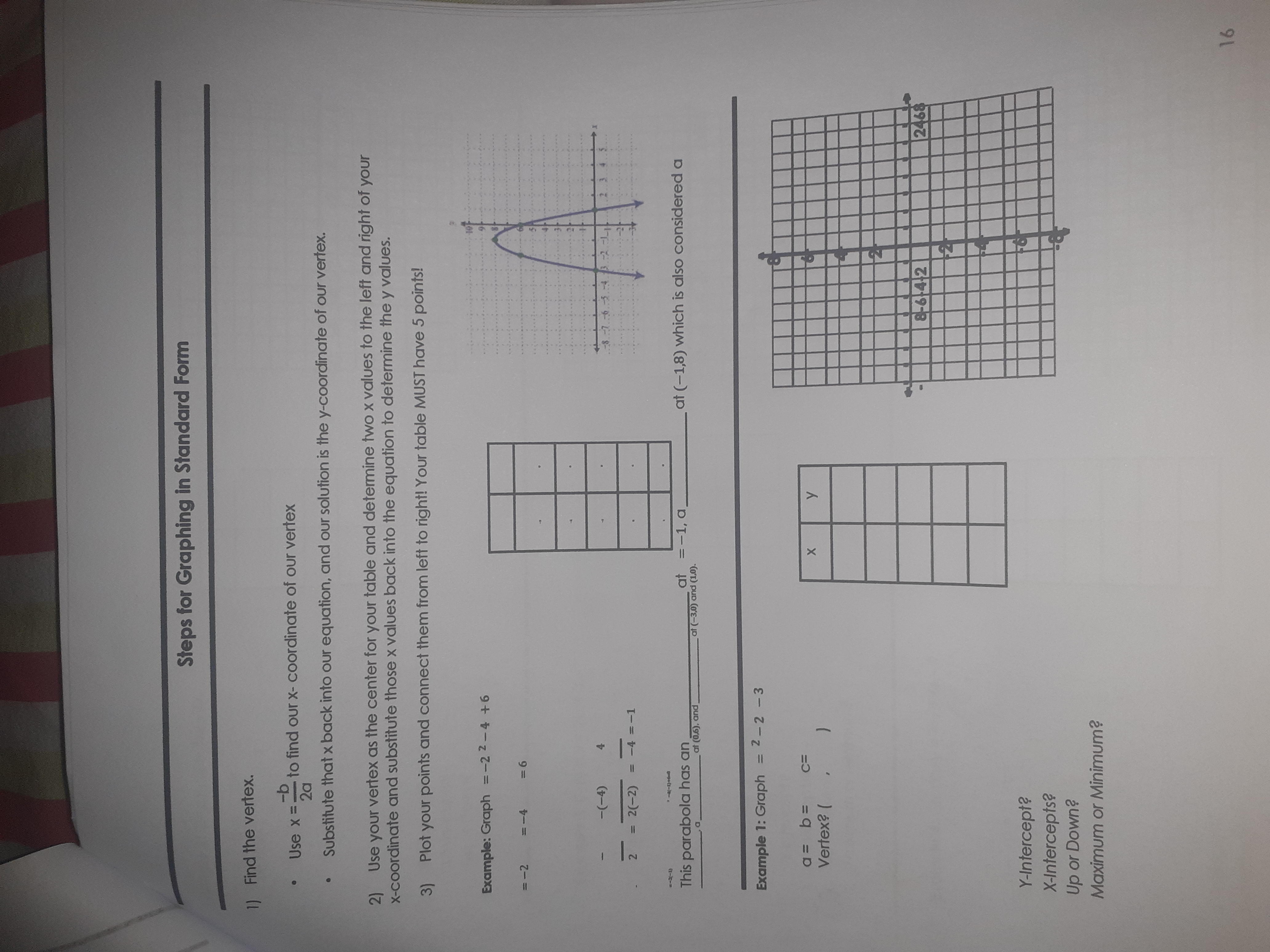
Day 5: Graphing Quadratic Functions in Standard Form Standard(s): MGSE9-12.F.IF.7 Graph functions expressed algebraically and show key features of the graph both by hand and by using technology. The parent function of a function is the simplest form of a function. The parent function for a quadratic function is y = x2 or f(x) = x2. Graph the parent function below. The U-shaped graph of a X X2 quadratic function is called a -3 -2 The highest or lowest point on -1 a parabola is called the O One other characteristic of a 2 quadratic equation is that one of the terms is always 3 Standard Form of a Quadratic Function: y = ax2 + box + c The is = - The is on the axis of symmetry line. Look for that x-value in your table. The a-value determines whether your graph "goes up" on both sides or "goes down" on both sides of your vertex. : a-value is positive (looks like a "U") : a-value is negative (looks like an "n") The are where = . You can either solve the equation + . to find the roots or look for where The in your table. is where = . This will be the paint ( . ). A good PARABOLA has at least five points. Make a table of values with your vertex in the middle and plot them to make a good graph. 15Steps for Graphing in Standard Form 1) Find the vertex. Use x = - to find our x- coordinate of our vertex 2 Substitute that x back into our equation, and our solution is the y-coordinate of our vertex. 2) Use your vertex as the center for your table and determine two x values to the left and right of your x-coordinate and substitute those x values back into the equation to determine the y values. 3) Plot your points and connect them from left to right! Your table MUST have 5 points! Example: Graph =-2 2-4 +6 =-2 =-4 =6 -(-4) 8. 7. 6.-3.-4 3. - 2 = 2(-2) = -4 =-1 This parabola has an at =-1, a at (0.6). and at (-1,8) which is also considered a - at (-3,0) and (1,0). Example 1: Graph = 2-2 -3 a = b= C= Vertex? ( X y 2468 Y-Intercept? X-Intercepts? Up or Down? Maximum or Minimum? 16Example 2: Graph: y = 3X2 - 6x. X a= b= c= Vertex? ( Y-Intercept? X-Intercepts? Up or Down? Maximum or Minimum? Example 3: Graph y = 2x2 + 3. a = b = X y Vertex? ( 8 - 6 Y-Intercept? X-Intercepts? Up or Down? Maximum or Minimum? Example 4: Graph: y = - X2 + 6x -9 a = b = C = x y Vertex? ( 8-6 4-2 2468 Y-Intercept? X-Intercepts? Up or Down? Maximum or Minimum? 17EXGID Day 6: Graphing Quadratic Functions (Vertex Form) Standard(s): MGSE9-12.F.IF.7 Graph functions expressed algebraically and show key features of the graph both by hand and by using technology. Vertex Form of a Quadratic Function y =a ( x - h)2+k Vertex: (h, k) The The -is (Opposite of h) is on the axis of symmetry line at ( , ). Remember: the sign of "h" is the opposite The a-value determines whether your graph "goes up" on both sides or "goes down" on both sides of your vertex. : a-value is positive (looks like a "U") : a-value is negative (looks like an "n") A good PARABOLA has at least five points. Make a table of values with your vertex in the middle and plot them to make a good graph. Transformations If the a-value is negative, your graph has been REFLECTED over the x-axis. If the a-value (ignoring the negative) is less than one, your graph has been SHRUNK or COMPRESSED vertically. If the a-value (ignoring the negative) is bigger than one, your graph has been STRETCHED vertically. The location of the vertex determines where the graph has been SHIFTED or TRANSLATED.Graphing in Vertex Form Example 1: Graph y = (x - 1)2 - 2. a = h = K = X y Vertex = ( Transformations? Up or Down? Maximum or Minimum? Example 2: Graph: y = -3(x + 4)2+ 1. a= h = k = X y Vertex = ( Transformations? -8 Up or Down? Maximum or Minimum? Example 3: Graph y = 2x2 + 3. a = h = K = Vertex = ( Transformations? -8 -6-4-22468-2 Up or Down? Maximum or Minimum