Please help me answer this. Thank you!

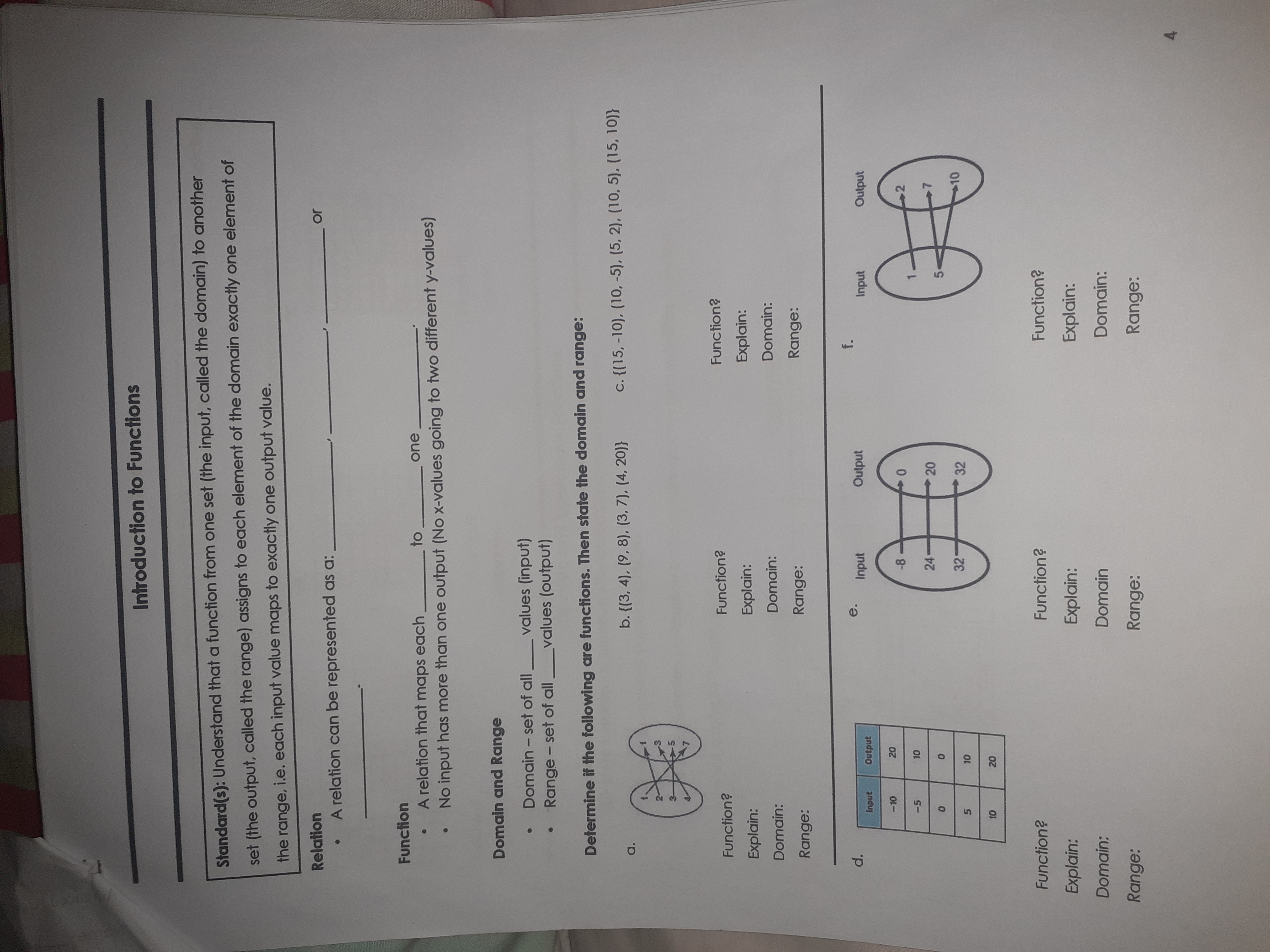
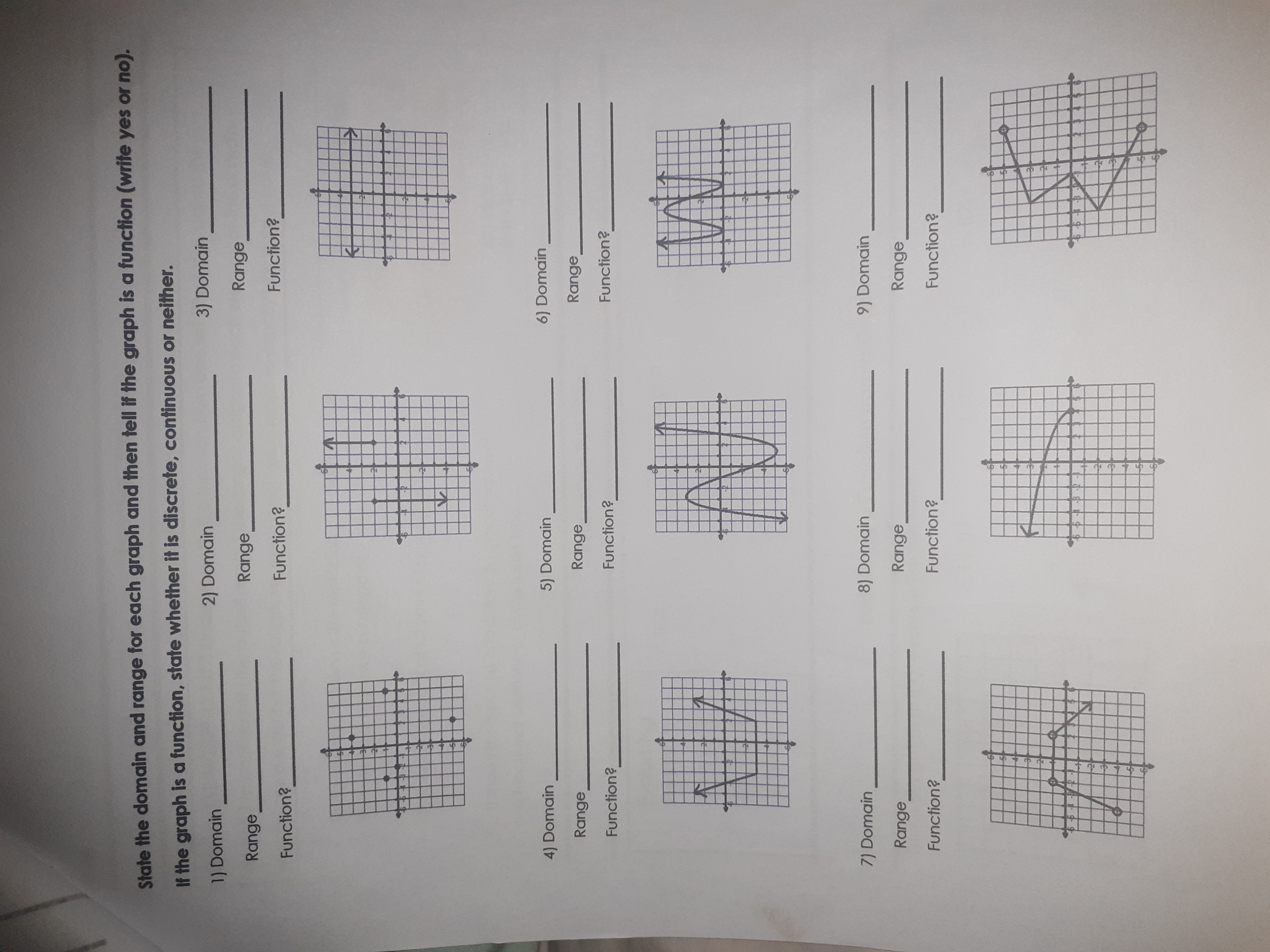
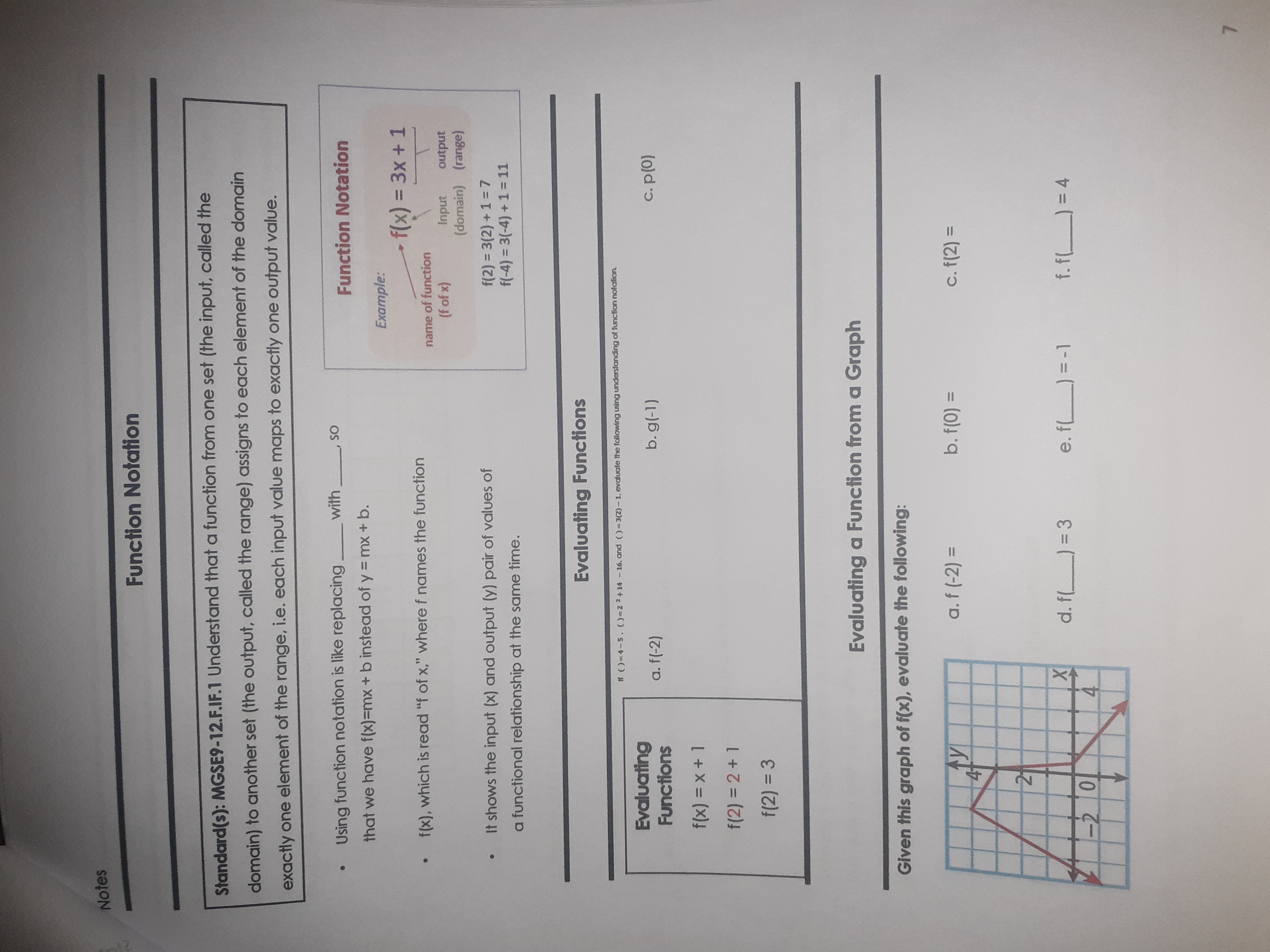
Introduction to Functions Standard(s): Understand that a function from one set (the input, called the domain) to another set (the output, called the range) assigns to each element of the domain exactly one element of the range, i.e. each input value maps to exactly one output value. Relation . A relation can be represented as a: Function . A relation that maps each to one No input has more than one output (No x-values going to two different y-values) Domain and Range Domain - set of all_ _ values (input) Range - set of all _values (output) Determine if the following are functions. Then state the domain and range: a . b. {(3, 4). (9, 8). (3, 7). (4, 20)} c. {(15, -10), (10, -5), (5, 2). (10, 5), (15, 10)} Function? Function? Function ? Explain: Explain: Explain: Domain: Domain: Domain: Range: Range: Range: e. Input Output f. Input Output Input Output -10 20 -5 10 0 5 10 10 20 Function? Function? Function? Explain: Explain: Explain: Domain: Domain Domain: Range: Range: Range:Vertical Line Test Consider all the vertical lines that could be drawn on the graph of the relation. If any of the vertical lines intersect the graph of the relation at more than one point, then the relation is not a function. Ex. Use the Vertical Line Test to determine if the graphs of the relations are functions. A. B . C. Function? Function ? Function? Explain: Explain: Explain: Discrete and Continuous Functions Discrete function - a function with distinct and separate values. Example: number of students at SCHS, Continuous function - a function that can take on any number within a certain interval. Example: height, age, time DISCRETE CONTINUOUS height customerState the domain and range for each graph and then tell if the graph is a function (write yes or no). If the graph is a function, state whether it is discrete, continuous or neither. 3) Domain 1) Domain 2) Domain Range Range Range Function? Function? Function? 4) Domain 5) Domain 6) Domain Range Range Range Function? Function? Function? 7) Domain 8) Domain 9) Domain Range Range Range Function? Function? Function?Notes Function Notation Standard(s): MGSE9-12.F.IF.1 Understand that a function from one set (the input, called the domain) to another set (the output, called the range) assigns to each element of the domain exactly one element of the range, i.e. each input value maps to exactly one output value. Using function notation is like replacing with_ So Function Notation that we have f(x)=mx + b instead of y = mx + b. Example: f (x) = 3x +1 f(x), which is read "f of x," where f names the function name of function (f of x) Input output (domain) (range) It shows the input (x) and output (y) pair of values of f(2) = 3(2) +1=7 a functional relationship at the same time. f(-4) = 3(-4) + 1 = 11 Evaluating Functions " ( )=4-5. ()=22+14 -16, and ()=3(2) - 1, evaluate the following using understanding of function notation. Evaluating Functions a. f(-2) b. g(-1) c. p(0) f ( x ) = x+ 1 f ( 2 ) = 2+ 1 f (2) = 3 Evaluating a Function from a Graph Given this graph of f(x), evaluate the following: a. f (-2) = b. f(0) = c. f(2) = 21 d. f(_) = 3 e. f() = -1 f. f ( ) = 4 10Applications of Evaluating Functions Scenario 1: While visiting her grandmother, Fiona Evans found markings on the inside of a closet door showing the heights of her mother, Julia, and her mother's brothers and sisters on their birthdays growing up. From the markings in the closet, Fiona wrote down her mother's height each year from ages 2 to 13. Her grandmother found the measurements at birth and one year by looking in her mother's baby book. The data is provided in the table below, with heights rounded to the nearest inch. Age O 10 121 13 (yrs. Height 30 (in.) 21 35 39 43 46 48 151 53 55 59 62 64 64 a. Which variable is the independent variable? Dependent variable? enolTony- b. What is h(11) and what does this mean in context? c. Express how tall her mother was at age 10 using function notation. d. What is a such that h(a)=53 and what does this mean in context? e. What would be an appropriate domain and range for this function? Scenario 2: You determine while walking home from school one day, you live approximately 3000 feet away from school and you can walk 5 feet every second. You determine the function d(1)=3000 - 51 models how far, d, you have left to walk after t seconds walking home. a. What is the independent variable? b. What is the dependent variable? c. How far will you be from home in one MINUTE? d. How long does it take you to be a HALF MILE from home? e. If you live 3000 feet from school, what would be an appropriate domain and range be for this situation