Please help me complete the tables and questions from the procedure.

Here's the link:

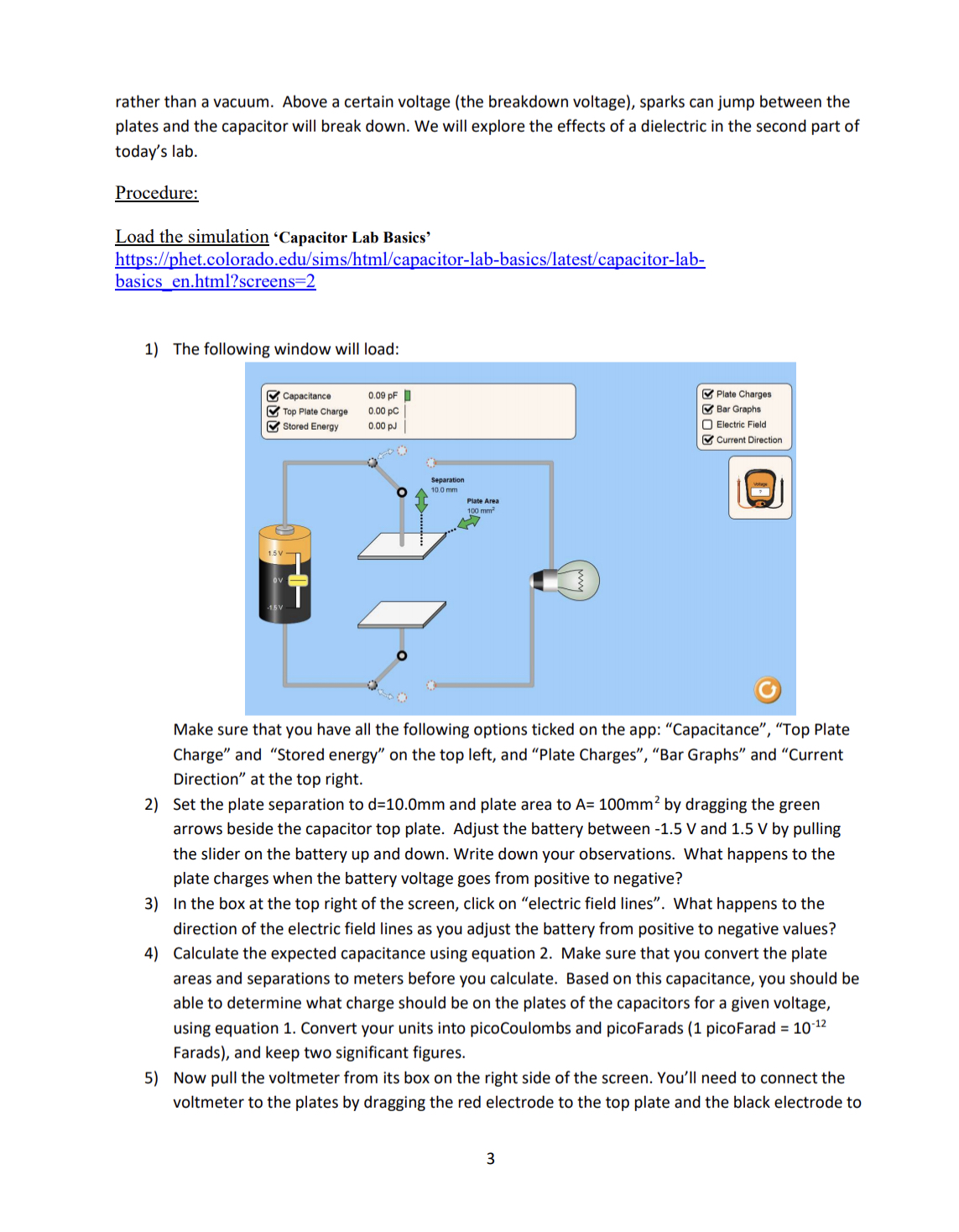
the bottom plate. Slide the bar on the battervto set the voltage as close as you can to the values shown in Ta bie 1, and make three measurements of Charge (1, and the corresponding voltage V. Calculate the experimental capacitance C=Q/V. Does it agree with the capacitance meter, and with what you found in step 4 (allowing for the number of significant figures shown in the app)? Does the capacitance change when you change the battery voltage? Why or why not? Table 1: Parallel Plate Capacitor V (Volts) 0. (picoCouiombs) Capacitance from Calculated meter (plcoFarads) Capacitance =QfV(pF] 6) Now we're going to investigate what happens when we change the dimensions of our capacitor. a) Varythe area of the plates by pulling in and out on the green arrow below the words \"Plate Area\". How does the capacitance vary with area A? If you increase the area, does the capacitance decrease or increase? b) Vary the separation of the plates. How does the capacitance vary with the separation d? If you decrease the separation, does the capacitance decrease or increase? c) Fill in Table 2, below by adjusting the area and separation to the values specified. The calculated capacitance in the last column should be calculated using equation 2. Do the measured and calculated capacitances agree with each other? Keep two signlflcant gures. rather than a vacuum. Above a certain voltage (the breakdown voltage), sparks can jump between the plates and the capacitor will break down. We will explore the effects of a dielectric in the second part of today's lab. Procedure: Load the simulation 'Capacitor Lab Basics' hgps:thetcolorado.edufsimsfhbnlfcawitor-lab-basicsatestfcapacitorlab- basics en.i11ml?scrccns=2 1) The following window will load: 2) 3) Make sure that you have all the following options ticked on the app: \"Capacitance\Table 2: Variation of Capacitance with Dimensions 7) Adjust the battery to 1.5 V. Set the plate separation to 10.0mm and the plate area to 100mm2. Tick the "Electric Field\" box, and electric field lines should appear. The number of electric field lines is proportional to the strength of the electric field. Watch what happens when the separation of the plates is increased. a) What happens to the charge when the plate separation is increased, and why? (Please take note of any charge flowthe large blue arrows in the lines connecting the battery and the capacitor) b) What happens to the strength of the eld when the separation is increased, and why? 8) With the separation set to 5 mm, and the area at lliiilmm2 disconnect the battery by pulling the wires from the top and bottom of the capacitor to the vertical position, as shown below. Pull the red probe of the voltmeter to the top plate and the black probe to the bottom plate. a) What happens to charge when the plate separation is Increased, and why? b) What happens to the voltage when the plate separation is increased, and why? (Note: you may have to drag the voltmeter probes around to reconnect them as the plate separation varies) c) What happens to the strength of the eld when plate separation is increased? (You can use the field meter to check this. ' Figure 2. Simple Parallel Plate Capacitor When the capacitor is charged, an electric field exists between the two plates, going from the positively charged plate to the negatively charged plate. The magnitude of this electric field is: VQQ === 3 0' Cd 60A H The amount of energy stored in the capacitor is proportional to the square of the electric eld, and is given by. 1 Q2 1 , PE= V==CV 4 29 2C 2 H One way to increase the amount of charge (i.e. energy) that can be stored in a capacitor is to insert a dielectric into the gap between the two plates. A dielectric is just an insulating material which has a permittivity, s greater than so. In general, emcee, where 101. Thus, when a dielectric is added, the capacitance will Increase by a factor of 1c, and thus the charge stored on the capacitor will also Increase by a factor of K. A A C: ; =CV= V 5 read Q K5,, d {i The total electric field in the capacitor for a given voltage and plate separation will not change, even though there is a larger electric charge built up on the metal plates. This is because there are now two electric elds presentone between the metal plates and one inside the dielectric. This is because the surfaces of the dielectric also have charges built up on them that opposed the increasing field from the metal plates. The dielectric has an internal electric field that opposes that of the metallic plates, and the total electric field remains constant. A drawback of a dielectric is that, because It consists of atoms rather than empty space, it is a lot easier for charges to flow between the positive and negative plates when they are separated by a dielectric Capacitors A capacitor is a circuit component which stores energy in the form of electric field. In its simplest form, it consists of two conducting plates, separated by an insulator. + +0 V ' ~Q Figure 1: Simple Capacitor Circuit When connected to a voltage source, current flows, and the two plates of the capacitor become oppositely charged {see Figure 1}. When the electric potential across the capacitor is equal to that from the voltage scurce, Current will stop flowing, and we say that the capacitor is fully charged. The amount of charge, 0, on the capacitor plates is related to the voltage, V, of the power source by the capacitance, C, of the capacitor, with the relationship Q=CV {ii The capacitance has units of Farads {F}, where 1F=1 Coulomb/Volt. Its magnitude depends on the area of the capacitor plates, A, their separation, d, and the material which separates the two plates. For this lab, we will consider only the simplest form of capacitor, the parallel plate capacitor, which consists of two metal plates separated by air as shown in Figure 2. In this capacitor, the capacitance ls given by: A (3:80; (2) Here .sia=8.85x10'12 Ffm is the permittivity of free Space. Clearly, this very small multiplicative constant means that the capacitance will be very small, unless the ratio Aid is very large. In fact, most capacitors used in circuits have values smaller than 1 microfarad, Le. 10' F. The capacitance can be increased either by increasing the plate area, or decreasing the plate separation