please help me solve these

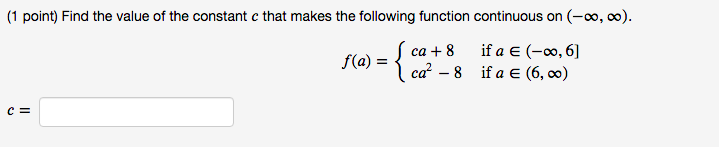
(1 point) A function f(x) is said to have a removable discontinuity at x = a if both of the following conditions hold: 1. f is either not defined or not continuous at x = a. 2. f(a) could either be defined or redefined so that the new function is continuous at x = a. Show that x' + 12x + 41 if x -6 has a removable discontinuity at x = -6 by (a) verifying (1) in the definition above, and then (b) verifying (2) in the definition above by determining a value of f(-6) that would make f continuous at x = -6. f(-6) = would make f continuous at x = -6. Now draw a graph of f(x). It's just a couple of parabolas!(1 point) A function f is said to have a removable discontinuity at a if: 1. f is either not defined or not continuous at a. 2. f(a) could either be defined or redefined so that the new function is continuous at a. Let f(x) = 2x-+3x-5 x-1 Show that f has a removable discontinuity at 1 and determine the value for f(1) that would make f continuous at 1. Need to redefine f(1) = 1(1 point) Find the value of the constant c that makes the following function continuous on (-co, co). f(a) = ca + 8 if a e (-oo, 6] cat - 8 if a E (6, 00) CE