Please help me solve this question

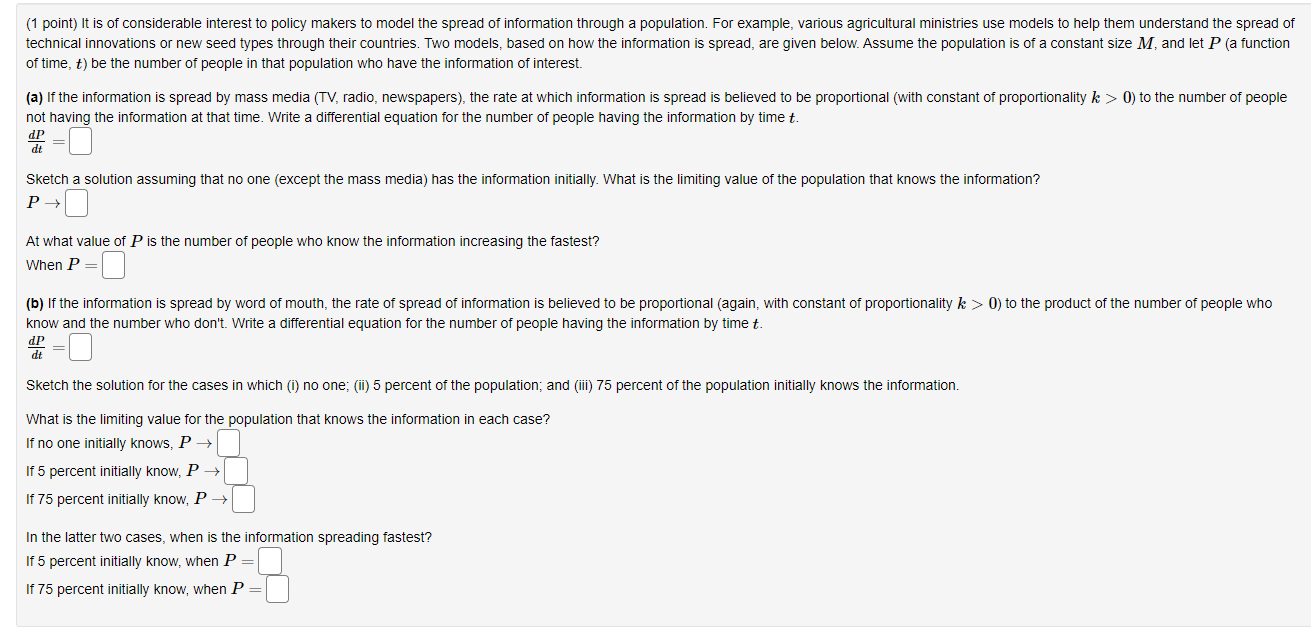
(1 point) A tumor spreads through a school. Let ya) be the fracon 0f the population that has heard the tumor at time t and assume that the rate at which the rumor spleads i5 proportionai t0 the product of the fraction yet the population that has heard the tumor and the flaction 1 ythat has not yet heard the rumor. The school has 1000 students in total. At 8 am, 107 students have heard the rumor, and Dy noon, half the school has heard it. Using the logistic model explained above determine how much time passes before 90% 0f the students Will have heard the rumor. 90% of the students have heard the rumor aer about U hours. (1 point) It is of considerable interest to policy makers to model the spread of information through a population For example, various agricultural ministries use models to help them understand the spread of technical innovations or new seed types through their countries. Two models, based on how the information is spread, are given below. Assume the population is of a constant size M, and let P (a function of time, t) be the number of people in that population who have the information of interest. (a) If the information is spread by mass media (TV, radio, newspapers), the rate at which information is spread is believed to be proportional (with constant of proportionality k > O) to the number of people not having the information at that time. Write a ditferential equation for the number of people haVing the information by time t Sketch a solution assuming that no one (except the mass media) has the information initially. What is the limiting value of the population that knows the information? P > D At what value of P is the number of people who know the information increasing the fastest? WhenP=D [b] If the information is spread by word of mouth, the rate of spread of information is believed to be proportional (again, with constant of proportionality .l: > 0) to the product of the number of people who know and the number who don't. Write a differential equation for the number of people having the information by time t. s , Cl dc , Sketch the solution forthe cases in which (i) no one; (ii) 5 percent of the population; and (iii) 75 percent of the population initially knows the information. What is the limiting value for the population that knows the information in each case'? If no one initially knows, P a If 5 percent initially Know, P a If 75 percent initially know. P > In the latter two cases, when is the information spreading fastest? If 5 percent initially Know, when P = If 75 percent in'rtially know, when P =