Please help me solve this two questions. Thanks!

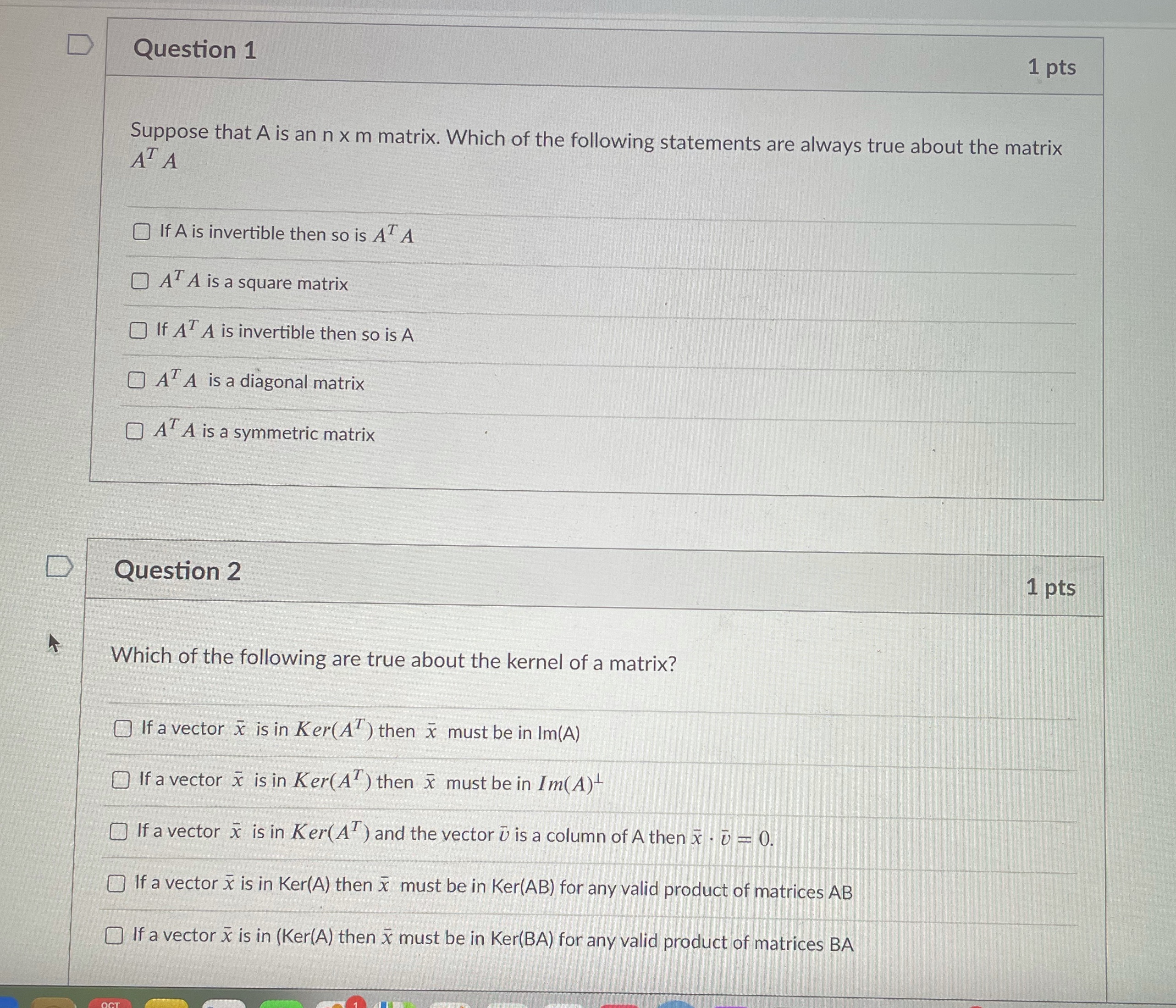
D Question 1 1 pts Suppose that A is an n x m matrix. Which of the following statements are always true about the matrix A A If A is invertible then so is AT A O AT A is a square matrix If AT A is invertible then so is A O AT A is a diagonal matrix O A'A is a symmetric matrix Question 2 1 pts Which of the following are true about the kernel of a matrix? If a vector x is in Ker(A ) then x must be in Im(A) If a vector x is in Ker(A' ) then x must be in Im(A) If a vector x is in Ker( A' ) and the vector i is a column of A then x . D = 0. If a vector x is in Ker(A) then x must be in Ker(AB) for any valid product of matrices AB If a vector x is in (Ker(A) then x must be in Ker(BA) for any valid product of matrices BA