Please help me.

The requested project is dealing with some analysis of 2D straight line geometric shapes. As you studied in your earlier stages, a straight line has many defining equation forms in 2D geometry. One famous equation for defining straight line is: + + = 0 while a, b and c are real numbers. Any 2 straight lines in the plane are either parallel (have no intersection point) or intersected in a point in the plane. If the two straight lines are defined as: 1 + 1 + 1 = 0 (1) 2 + 2 + 2 = 0 (2) The two straight lines are considered parallel if: 12 = 21. The two straight lines are considered not parallel and intersected in an intersection point ( , ) where 12 21 and in this case the coordinates of the intersection point and are defined as: ( , ) = ( 1221 1221 , 1221 1221 ) (3) Implement a Java program that reads from the user the 6 coefficient values of the 2 straight lines 1, 1, 1 and 2, 2, 2 (for minimum 20 pairs of straight lines.) The program checks, for each pair, if they are parallel or intersected. If, for each pair, they are intersected, the program has to computer the coordinates of the intersection point as given in equation 3. Finally, the program should print the number and percent ratio (rounded to 2 decimal places) of: o Parallel straight line pairs. o Intersected straight line pairs. o Intersected straight line pairs with intersection point on x-axis or y-axis. o Intersected straight line pairs with intersection point in first plane quadrant.

o Intersected straight line pairs with intersection point in second plane quadrant. o Intersected straight line pairs with intersection point in third plane quadrant. o Intersected straight line pairs with intersection point in fourth plane quadrant

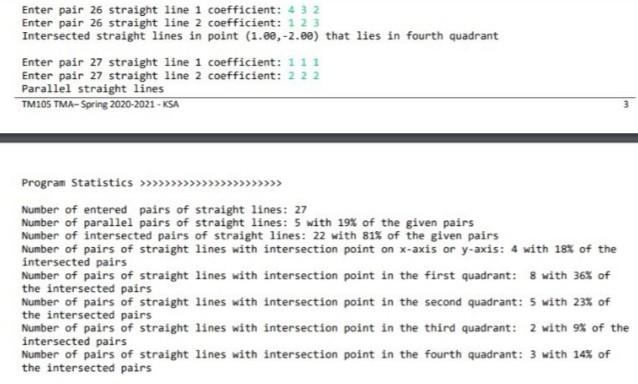
OVERVIEW The requested project is dealing with some analysis of 2D straight line geometric shapes. As you studied in your earlier stages, a straight line has many defining equation forms in 20 geometry. One famous equation for defining straight line is: ax + by + c = 0 while a, b and care real numbers Any 2 straight lines in the plane are either parallel (have no intersection point) or intersected in a point in the plane. If the two straight lines are defined as: 2x +by+4 = 0 (1) 22x+by+c, = 0 (2) The two straight lines are considered paralett: az b2 = azba The two straight lines are considered not parallel and intersected in an intersection point (...) where a, b, a, b, and in this case the coordinates of the intersection point and are defined as: (bc-b2c1902-C301) lab-a2b, aby-a2017 Implement a Java program that reads from the user the 6 coefficient values of the 2 straight lines ab anda, b2, C (for minimum 20 pairs of straight lines.) The program checks, for each pair, if they are parallel or intersected. M, for each pair, they are intersected, the program has to computer the coordinates of the intersection point as given in equation 3. Finally, the program should print the number and percent ratio (rounded to 2 decimal places) ot: o Parallel straight line pairs. o Intersected straight line pairs. Intersected straight line pairs with intersection point on x-axis or yaxis. o Intersected straight line pairs with intersection point in first plane quadrant (3) Intersected straight line pairs with intersection point in second plane quadrant Intersected straight line pairs with intersection point in third plane quadrant Intersected straight line pairs with intersection point in fourth piane quadrant. Note: You may use digital library or internet to check each case of intersection point coordinates. The program should work like as puen sample run. Sample Run: Enter number of straight line pairs: 12 Minimum accepted number of straight line pairs is 20 Enter number of straight line pairs: 27 Enter pair 1 straight line 1 coefficient: 134 Enter pair 1 straight line 2 coefficient: 213 Intersected straight lines in point (-1.88,-1.80) that lies in third quadrant Enter pair 2 straight line 1 coefficient: 251 Enter pair 2 straight line 2 coefficient: 313 Intersected straight lines in point (-1.88,8.23) that lies in second quadrant Enter pair 3 straight line 1 coefficient: 222 Enter pair 3 straight line 2 coefficient: 314 Intersected straight lines in point (-1.58,0.58) that lies in second quadrant Enter pair 26 straight line 1 coefficient: 4 3 2 Enter pair 26 straight line 2 coefficient: 1 2 3 Intersected straight lines in point (1.98,-2.88) that lies in fourth quadrant Enter pair 27 straight line 1 coefficient: 111 Enter pair 27 straight line 2 coefficient: 222 Parallel straight lines TM105 TMA-Spring 2020-2021 - KSA Program Statistics >>>>>>>>>>>>>>>>>>>>>>> Number of entered pairs of straight lines: 27 Number of parallel pairs of straight lines: 5 with 19% of the given pairs Number of intersected pairs of straight lines: 22 with 81% of the given pairs Number of pairs of straight lines with intersection point on x-axis or y-axis: 4 with 18% of the intersected pairs Number of pairs of straight lines with intersection point in the first quadrant: 8 with 36% of the intersected pairs Number of pairs of straight lines with intersection point in the second quadrant: 5 with 23% of the intersected pairs Number of pairs of straight lines with intersection point in the third quadrant: 2 with 9% of the intersected pairs Number of pairs of straight lines with intersection point in the fourth quadrant: 3 with 14% of the intersected pairs