Please help me with my home work answer all the questions below. Thanks a lot!

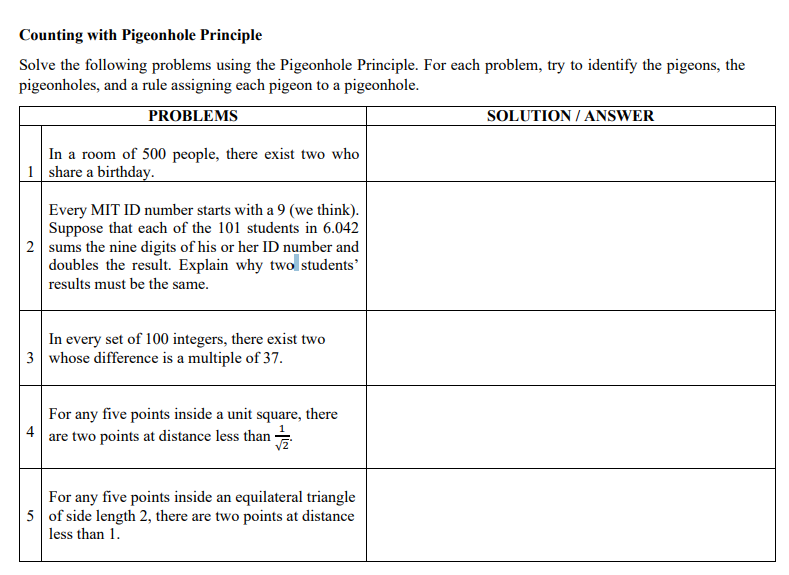
Counting with Pigeonhole Principle Solve the following problems using the Pigeonhole Principle. For each problem, try to identify the pigeons, the pigeonholes, and a rule assigning each pigeon to a pigeonhole. PROBLEMS SOLUTION / ANSWER In a room of 500 people, there exist two who 1 share a birthday. Every MIT ID number starts with a 9 (we think). Suppose that each of the 101 students in 6.042 2 sums the nine digits of his or her ID number and doubles the result. Explain why two students' results must be the same. In every set of 100 integers, there exist two 3 whose difference is a multiple of 37. 4 For any five points inside a unit square, there are two points at distance less than a For any five points inside an equilateral triangle 5 of side length 2, there are two points at distance less than 1