Please help me with my practice quiz for Statics for Managers. Images are attached. Thank you,

(1) In hypothesis testing, we can minimize the probability of making a Type I error by: (check all that are correct.)

(2) If the alternate hypothesis states that ? NOT= 4,000, where is the rejection region for the hypothesis test?

(3) Given: For a two-tailed test and alpha = 0.01, the z critical values are -2.576 and +2.576. If the calculated z-test statistic is found to be 6.00, which of the following would be the correct decision?

(4) A hypothesis regarding the weight of football players is that the mean is 255 pounds. A sample of 12 players are selected and their weights are taken, and the mean and standard deviation is calculated from the sample. In order to test the hypothesis above, which test statistic would you use?

(5) The daily high temperature for Kawai'I is normally distributed with a known population standard deviation of 7. What is a 95% confidence interval if a sample of 100 days is taken and the mean is 87?

(6) If we want to test the hypothesis that the 2 samples in a paired sample have the same mean which test statistic would I use?

(7) When testing for the difference between 2 population means you are given: Sample 1: n1 = 24, mean1 = 130, s1 = 19; Sample 2: n2 = 28, mean2 = 125, s2 = 17.5. What distribution do we use to find the critical value?

(8) When building a confidence interval for the difference between 2 population means that have equal and unknown variances you are given: Sample 1: n1 = 24, mean1 = 130, s1 = 19; Sample 2: n2 = 28, mean2 = 125, s2 = 17.5. What is the pooled standard deviation you use when making the confidence interval?

(9) When building a 95% confidence interval for the difference between 2 population means that have equal and unknown variances you are given: Sample 1: n1 = 24, mean1 = 130, s1 = 19; Sample 2: n2 = 28, mean2 = 125, s2 = 17.5. The difference in the means is 5. How much do you add and subtract to 5 to get a confidence interval (i.e. what is the margin of error)?

(10) We are testing - does the Firestone AB tire get more mileage before needing to be replaced than the Goodyear CD tire? Let muAB = Firestone AB population mean mileage. Let muCD = Goodyear population mean mileage. Select the properly constructed null hypothesis.

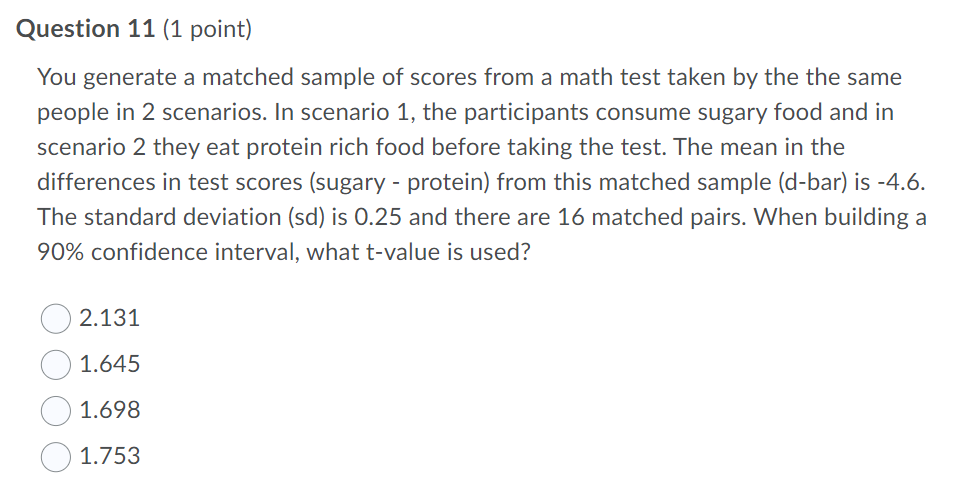
(11) You generate a matched sample of scores from a math test taken by the the same people in 2 scenarios. In scenario 1, the participants consume sugary food and in scenario 2 they eat protein rich food before taking the test. The mean in the differences in test scores (sugary - protein) from this matched sample (d-bar) is -4.6. The standard deviation (sd) is 0.25 and there are 16 matched pairs. When building a 90% confidence interval, what t-value is used?

(12) You generate a matched sample of scores from a math test taken by the the same people in 2 scenarios. In scenario 1, the participants consume sugary food and in scenario 2 they eat protein rich food before taking the test. The mean in the differences in test scores (sugary - protein) from this matched sample (d-bar) is -4.6. The standard deviation (sd) is 0.25 and there are 16 matched pairs. When building a 90% confidence interval, what value do you add and subtract to -4.6 to build the confidence interval (what is the margin of error)?

(13) When testing for the difference between 2 population proportions, what test statistic is used as the critical value? Assume there are 41 observations from sample 1 and sample 2. You want to use a 90% confidence level, or 10% for a 2 tail test.

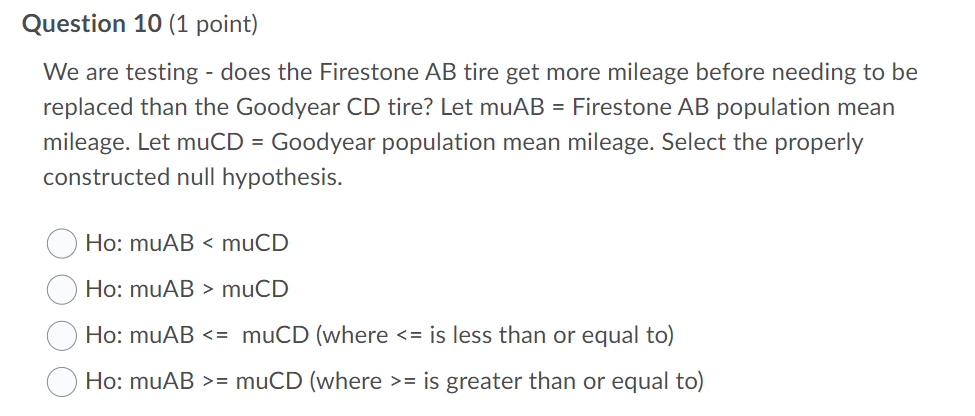
Question 1 (4 points] In hypothesis testing, we can minimize the probability of making a Type I error by: (check all that are correct.) C] Choosing a small p-value as a critical p. C] Minimizing the critical value from the z or t-table. C] Maximizing rejection region. Q Selecting a smaller alpha. Question 2 (1 point) If the alternate hypothesis states that 0 NOT= 4,000, where is the rejection region for the hypothesis test? 0 In the lowerUeft] tail 0 In both tails O In the area between the tails O In the upper (right) tail Question 10 (1 point) We are testing - does the Firestone AB tire get more mileage before needing to be replaced than the Goodyear CD tire? Let muAB = Firestone AB population mean mileage. Let muCD = Goodyear population mean mileage. Select the properly constructed null hypothesis. Ho: muAB muCD O Ho: muAB = muCD (where >= is greater than or equal to)Question 11 (1 point) You generate a matched sample of scores from a math test taken by the the same people in 2 scenarios. In scenario 1, the participants consume sugary food and in scenario 2 they eat protein rich food before taking the test. The mean in the differences in test scores (sugary - protein) from this matched sample {d-barl is 4.6. The standard deviation (sd) is 0.25 and there are 16 matched pairs. When building a 90% confidence interval, what t-value is used? Question 12 (1 point) You generate a matched sample of scores from a math test taken by the the same people in 2 scenarios. In scenario 1, the participants consume sugary food and in scenario 2 they eat protein rich food before taking the test. The mean in the differences in test scores (sugary - protein) from this matched sample (d-bar) is -4.6. The standard deviation (sd) is 0.25 and there are 16 matched pairs. When building a 90% confidence interval, what value do you add and subtract to -4.6 to build the confidence interval (what is the margin of error)? Question 13 (1 point) When testing for the difference between 2 population proportions, what test statistic is used as the critical value? Assume there are 41 observations from sample 1 and sample 2. You want to use a 90% confidence level, or 10% for a 2 tail test. Question 3 (1 point) Given: For a two-tailed test and alpha = 0.01, the 2 critical values are -2.576 and +2576. If the calculated z-test statistic is found to be 6.00, which of the following would be the correct decision? 0 Reject H1 (alternative). 0 Do not reject HO (null). O Reject H0 (null). 0 Accept H0 (null). Question 4 (1 point) A hypothesis regarding the weight of football players is that the mean is 255 pounds. A sample of 12 players are selected and their weights are taken, and the mean and standard deviation is calculated from the sample. In order to test the hypothesis above, which test statistic would you use? 0 Chi-square test statistic O t-test statistic O F-test statistic O z-test statistic Question 5 (1 point) The daily high temperature for Kawai'l is normally distributed with a known pepulation standard deviation of 7. What is a 95% confidence interval if a sample of 100 days is taken and the mean is 87? O 85.20 - 88.80 0 85.63 - 88.37 0 85.85 - 88.15 0 86.86 - 87.14 Question 6 (1 point) If we want to test the hypothesis that the 2 samples in a paired sample have the same mean which test statistic would I use? 0 Paired F-test O Paired t-test O z-test 0 Test of the pooled standard deviations Question 7 (1 point) When testing for the difference between 2 population means you are given: Sample 1: n1 = 24, mean1 = 130,51 = 19; Sample 2: n2 = 28, mean2 = 125,52 = 17.5. What distribution do we use to find the critical value? 0 t-distribution with 50 degrees of freedom. 0 t-distribution with 51 degrees of freeedom. O z-distribution with 27 degrees of freeedom. O t-distribution with 26 degrees of freeedom. Question 8 (1 point) When building a confidence interval for the difference between 2 population means that have equal and unknown variances you are given: Sample 1: n1 = 24, mean1 = 130, 51 = 19; Sample 2: n2 = 28, mean2 = 125,52 = 17.5. What is the pooled standard deviation you use when making the confidence interval? Question 9 (1 point) When building a 95% confidence interval for the difference between 2 population means that have equal and unknown variances you are given: Sample 1: n1 = 24, meanl = 130,51 = 19; Sample 2: n2 = 28, mean2 = 125,52 = 17.5. The difference in the means is 5. How much do you add and subtract to 5 to get a confidence interval (i.e. what is the margin of error)