Please help me with this college assignment for Assembly language x86 (YASM)

Thank you

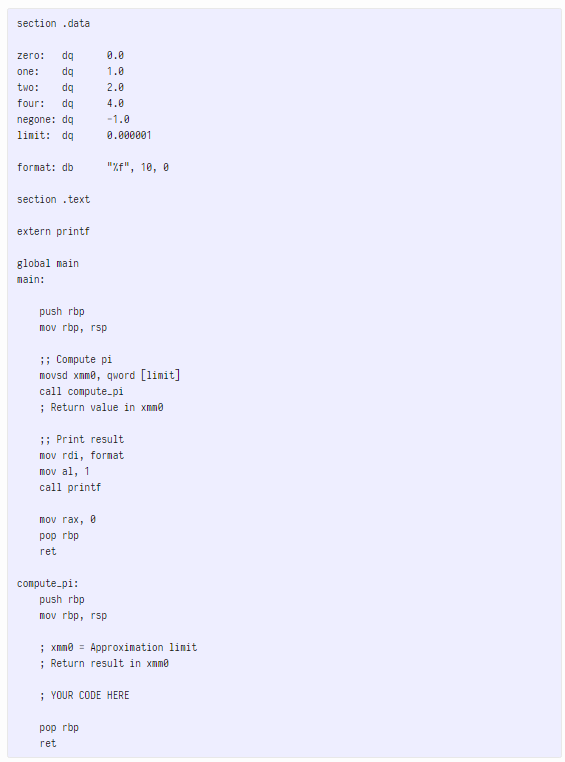
4 4 1 = 3+ (-1)' = 3+ (21+ 2)(2i+3)(21+4) 2 X3 X4 + i=0 This series converges much faster than the traditional one: while the traditional series takes nearly 500,00 iterations to get just five digits of precision, this series gets there in about 12. The other change we're going to make is for the approximation limit to be a parameter to the function, rather than a fixed constant, and for the function to printf its results after each iteration, so we can see the convergence happening. Here's a skeleton program for you: section .data zero: dg one: da two: da four: da negone: da limit: da 0.0 1.0 2.0 4.0 -1.0 0.000001 format: db "X", 10, section .text extern printf global main main: push rbp mov rbp, rsp ;; Compute pi movsd xnno, qword [limit] call compute-pi ; Return value in xmno i Print result mov rdi, format mov al, 1 call printf mov rax, pop rbp ret compute-pi: push rbp mov rbp, rsp ; xmnQ = Approximation limit ; Return result in xmmo ; YOUR CODE HERE pop rbp ret Note that I've changed all the constants to quords (i.e., double s), so don't forget to use the double-precision versions of the various operations. It should be possible to change the limit in the .text section to get more (or less) precise approximations. 4 4 1 = 3+ (-1)' = 3+ (21+ 2)(2i+3)(21+4) 2 X3 X4 + i=0 This series converges much faster than the traditional one: while the traditional series takes nearly 500,00 iterations to get just five digits of precision, this series gets there in about 12. The other change we're going to make is for the approximation limit to be a parameter to the function, rather than a fixed constant, and for the function to printf its results after each iteration, so we can see the convergence happening. Here's a skeleton program for you: section .data zero: dg one: da two: da four: da negone: da limit: da 0.0 1.0 2.0 4.0 -1.0 0.000001 format: db "X", 10, section .text extern printf global main main: push rbp mov rbp, rsp ;; Compute pi movsd xnno, qword [limit] call compute-pi ; Return value in xmno i Print result mov rdi, format mov al, 1 call printf mov rax, pop rbp ret compute-pi: push rbp mov rbp, rsp ; xmnQ = Approximation limit ; Return result in xmmo ; YOUR CODE HERE pop rbp ret Note that I've changed all the constants to quords (i.e., double s), so don't forget to use the double-precision versions of the various operations. It should be possible to change the limit in the .text section to get more (or less) precise approximations