Please help me with this problem!

Problem 6: The radius in the figure below varies with axial position based on the equation R(z):

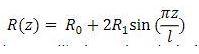
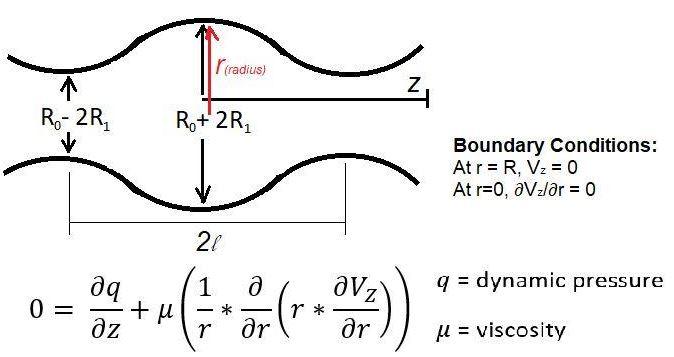
Where ₀ = mean radius, 2₁ = Amplitude, 2 = Period and Q = volumetric flow rate is specified. The density and viscosity of the fluid are constant.

a) Determine the velocity () assuming the conditions of lubrication approximation be applicable

HINT: The solution should be:

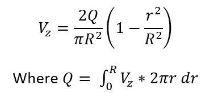
R(z)=R0+2R1sin(lz) Boundary Conditions: At r=R,Vz=0 At r=0,Vz/r=0 0=zq+(r1r(rrVZ))q=dynamicpressure=viscosity Vz=R22Q(1R2r2) nere Q=0RVz2rdr R(z)=R0+2R1sin(lz) Boundary Conditions: At r=R,Vz=0 At r=0,Vz/r=0 0=zq+(r1r(rrVZ))q=dynamicpressure=viscosity Vz=R22Q(1R2r2) nere Q=0RVz2rdr