Please help me write a code for this problem in Fortran. Here are some f90 files that I was given. If possible, PLEASE add notes to each line of code to explain the process. Thanks!

WATER_TANK_MASS_CONSERVATION.f90

Module my_subs implicit none ! ! (Declare Shared data here) ! real, parameter :: V_in=5, A_in=0.0025, A_exit=0.0025, g=9.8, A_tank=0.1 real :: V_exit ! contains Subroutine sub_rhs(rhs_1, h, time) implicit none real :: rhs_1, h, time V_exit=sqrt(2.*g*h) rhs_1=(V_in*A_in-V_exit*A_exit)/A_tank end subroutine sub_rhs end Module my_subs ! ! Program Main Use my_subs implicit none real :: del_t, rhs, time_total,t,h real, dimension(:), allocatable :: height, time, V_e integer :: i, i_max i_max=1000 time_total=200. del_t=time_total/Real(i_max) t=0.d0 h=1.d0 allocate (height(0:i_max),time(0:i_max), V_e(0:i_max)) height(0)=h time(0)=t V_e(0)=0.d0 do i=1,i_max call sub_rhs(rhs,h,t) h=h+rhs*del_t t=t+del_t print *,t,h time(i)=t height(i)=h v_e(i)=V_exit enddo open(1, file='out.dat') write(1,*)'Variables = "time" "height" "Vexit"' write(1,*)'Zone Datapacking = point' do i=0,i_max write(1,*)time(i),height(i),V_e(i) enddo stop end program main

WATER_TANK_ENERGY_CONSERVATION.f90

Module my_subs implicit none ! ! (Declare Shared data here) ! real, parameter :: V_in=5., A_in=0.0025, A_exit=0.0025, g=9.8, A_tank=0.1 real, parameter :: T_in=85. real :: V_exit, T_tank ! contains Subroutine sub_rhs(rhs_1,rhs_2, h, time) implicit none real :: rhs_1,rhs_2, h, time V_exit=sqrt(2.*g*h) rhs_1=(V_in*A_in-V_exit*A_exit)/A_tank rhs_2=(v_in*A_in*T_in-V_exit*A_exit*T_tank)/A_tank end subroutine sub_rhs end Module my_subs ! ! Program Main Use my_subs implicit none real :: del_t, rhs_1,rhs_2, time_total, t,h,h_Ttank real, dimension(:), allocatable :: height, time, V_e, T_e integer :: i, i_max i_max=1000 time_total=200. del_t=time_total/Real(i_max) t=0. h=1. T_tank=20. h_Ttank=h*T_Tank allocate (height(0:i_max),time(0:i_max), V_e(0:i_max),T_e(0:i_max)) height(0)=h time(0)=t V_e(0)=0. T_e(0)=T_tank do i=1,i_max call sub_rhs(rhs_1,rhs_2,h, t) h=h+rhs_1*del_t h_Ttank=h_Ttank+rhs_2*del_t t=t+del_t T_tank=h_Ttank/h print *,t,h,T_tank time(i)=t height(i)=h v_e(i)=V_exit T_e(i)=T_tank enddo open(1, file='out.dat') write(1,*)'Variables = "time" "height" "Vexit" "Ttank"' write(1,*)'Zone Datapacking = point' do i=0,i_max write(1,*)time(i),height(i),V_e(i),T_e(i) enddo stop end program main

PUMP.f90

Module Global_Data implicit none real, parameter:: Pi=3.14159265358979, densit=998., ks=0.000046, D1=0.10226,D2=0.0525018, viscos=0.001 real ::Q, V1,V2,Re1,Re2,A1=pi*D1**2/4.,A2=pi*D2**2/4.,f1,f2,rough1,rough2 real :: bhp_ref=7.5,pump_efficiency=0.75 real::f, Re, roughness real:: alpha=0.5 integer:: iter_max=100 end Module Global_Data ! ! Module Functions Use Global_data implicit none contains subroutine func(function_value,x) real:: x,function_value function_value=1/sqrt(x)+2.*log10(roughness/3.7+2.51/Re/sqrt(x)) return end subroutine func ! subroutine func_Prime(dfdx,x) real:: x,dfdx dfdx=-1/(2.*x**1.5) + 1/(-2.3025850929940463*x - 0.24793637267083515*x**1.5*Re*roughness) return end subroutine func_Prime ! end Module Functions

! Module inter_Solver use functions implicit none contains subroutine Newton_Raphson(icount,x,x_guess) implicit none real:: x,x_guess,f,dfdx,del_x integer:: icount x=x_guess do icount=1,iter_max call func(f,x) call func_prime(dfdx,x) del_x =-f/dfdx x=x+del_x*alpha ! print *,icount,abs(del_x) if(abs(del_x) iter_max)then print *,'Newton-Raphson method failed' else ! print *,'Newton-Raphson method' ! print *,'number of iterations =',iteration,' the solution is =', f1 endif ! f_guess=0.001 Re=Re2 roughness=rough2 call Newton_Raphson(iteration,f2,f_guess) if(iteration > iter_max)then print *,'Newton-Raphson method failed' else ! print *,'Newton-Raphson method' ! print *,'number of iterations =',iteration,' the solution is =', f2 endif h=6.4+6.98*f1*V1**2+4.443*f2*V2**2+0.452*V1**2+0.21*V2**2 bhp=998*Q*9.8*h /pump_efficiency/745.7 print *,998*Q*9.8*h,998*Q*9.8*h/745.7,bhp return end subroutine func_Q end Module Functions_Q ! Module exter_Solver use functions_Q implicit none contains ! subroutine Secant_Q(icount,x,x_1,x_2) implicit none real:: x,x_1,x_2,f_1,f_2,del_x integer:: icount x=x_1 call func_Q(f_1, x_1) call func_Q(f_2, x_2) do icount=1,iter_max del_x =(bhp_ref-f_1)*(x_2-x_1)/(f_2-f_1) x=x+del_x*alpha if(abs(del_x) iter_max)then print *,'Secant method for flow rate failed' else print *,iteration,Q endif print *,Q,Q_1,Q_2 stop end program main

MOODY.f90

Module Global_Data implicit none double precision, parameter:: alpha=0.5d0,Pi=3.14159265358979d0, & & densit=998., viscos=0.001 double precision::f, Re, roughness integer:: iter_max=100 end Module Global_Data ! ! Module Functions Use Global_data implicit none contains subroutine x_equals_to(x) implicit none double precision::x x=1./(-2.*log10(roughness/3.7+2.51/Re/sqrt(x)))**2 return end subroutine x_equals_to ! subroutine func(function_value,x) implicit none double precision:: x,function_value function_value=1/sqrt(x)+2.*log10(roughness/3.7+2.51/Re/sqrt(x)) return end subroutine func ! subroutine func_Prime(dfdx,x) implicit none double precision:: x,dfdx dfdx=-1/(2.*x**1.5) + 1/(-2.3025850929940463*x - 0.24793637267083515*x**1.5*Re*roughness) return end subroutine func_Prime end Module Functions ! ! Module Solver use functions implicit none contains subroutine Direct_substitution(icount,x_1,x) implicit none double precision:: x,x_1,x_old integer:: icount x=x_1 do icount=1,iter_max x_old=x call x_equals_to(x) ! print *,icount,abs(x-x_old) if(abs(x-x_old) iter_max)then print *,'Direct Substitution failed' else print *,'Direct Substitution' print *,'number of iterations =',iteration,' the solution is =', f endif !---------------------- Secant Method------------------ f_1=0.001 f_2=0.002 call Secant(iteration,f_1,f_2,f) if(iteration > iter_max)then print *,'Secant method failed' else print *,'Secant method' print *,'number of iterations =',iteration,' the solution is =', f endif !---------------------- Newton Raphson Method------------------ f_1=0.001 call Newton_Raphson(iteration,f_1,f) if(iteration > iter_max)then print *,'Newton-Raphson method failed' else print *,'Newton-Raphson method' print *,'number of iterations =',iteration,' the solution is =', f endif stop end program main

10hp.f90

Module Global_Data implicit none double precision, parameter:: Pi=3.14159265358979,gallon_to_m_cubic= 0.003785411784 double precision, parameter::D=0.05,ks=0.00026,den=998.,vis=0.001, L=1000. double precision::f, Re, roughness, V double precision:: alpha=0.5 integer:: iter_max=100 end Module Global_Data ! ! Module Functions Use Global_data implicit none contains subroutine x_equals_to(x) implicit none double precision::x x=1./(-2.*log10(roughness/3.7+2.51/Re/sqrt(x)))**2 return end subroutine x_equals_to ! subroutine func(function_value,x) implicit none double precision:: x,function_value function_value=1/sqrt(x)+2.*log10(roughness/3.7+2.51/Re/sqrt(x)) return end subroutine func ! subroutine func_Prime(dfdx,x) implicit none double precision:: x,dfdx dfdx=-1/(2.*x**1.5) + 1/(-2.3025850929940463*x - 0.24793637267083515*x**1.5*Re*roughness) return end subroutine func_Prime

subroutine Newton_Raphson(icount,x_guess,x) implicit none double precision:: x,x_guess,f,dfdx,del_x integer:: icount x=x_guess do icount=1,iter_max call func(f,x) call func_prime(dfdx,x) del_x =-f/dfdx x=x+del_x*alpha if(abs(del_x)

subroutine Cal_Power(D,Q,P) implicit none double precision::Q,P,f_1,f,delp,D integer::iteration, iter_max=100 V=Q/(Pi*D**2/4.) Re=den*V*D/vis roughness=ks/D f_1=0.001 call Newton_Raphson(iteration,f_1,f) if(iteration > iter_max)then print *,'Newton-Raphson method failed' stop endif delp=f*L/D*(0.5*den*V**2) P=delp*Q/745.7 return end subroutine Cal_power

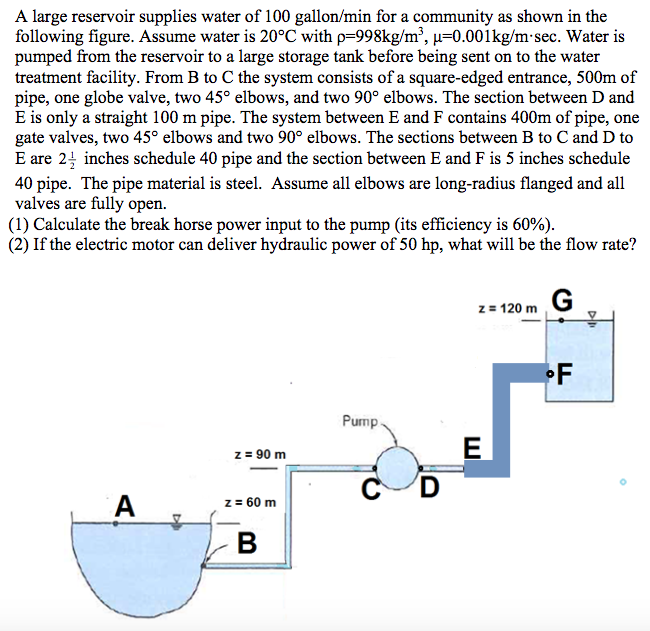
end Module Functions ! ! Module Solver use functions implicit none contains subroutine Secant(icount,D,Q_1,Q_2,P_1,P_ref) implicit none double precision:: Q,Q_1,Q_2,P_1,P_2,del_Q,P_ref,D integer:: icount Q=Q_1 call cal_power(D,Q_1,P_1) call cal_power(D,Q_2,P_2) do icount=1,iter_max del_Q =(P_ref-P_1)*(Q_1-Q_2)/(P_1-P_2) Q=Q+del_Q*alpha if(abs(P_1-P_ref) A large reservoir supplies water of 100 gallon/min for a community as shown in the following figure. Assume water is 20C with p-998kg/m3, =0.001 kg/m. sec. Water is pumped from the reservoir to a large storage tank before being sent on to the water treatment facility. From B to C the system consists of a square-edged entrance, 500m of pipe, one globe valve, two 45 elbows, and two 90 elbows. The section between D and E is only a straight 100 m pipe. The system between E and F contains 400m of pipe, one gate valves, two 45 elbows and two 90 elbows. The sections between B to C and D to E are 24 inches schedule 40 pipe and the section between E and F is 5 inches schedule 40 pipe. The pipe material is steel. Assume all elbows are long-radius flanged and all valves are fully open. (1) Calculate the break horse power input to the pump (its efficiency is 60%) (2) If the electric motor can deliver hydraulic power of 50 hp, what will be the flow rate? z 120 m oF urm