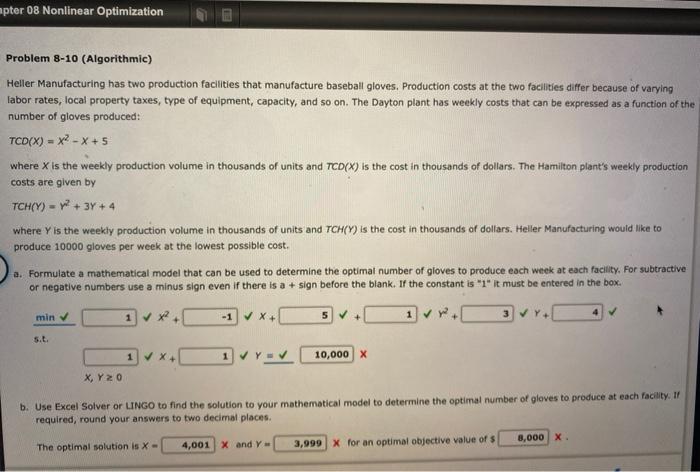
Question: please help please help Problem 8-10 (Algorithmic) Heller Manufacturing has two production facilities that manufacture baseball gloves. Production costs at the two facilities differ because
please help

please help
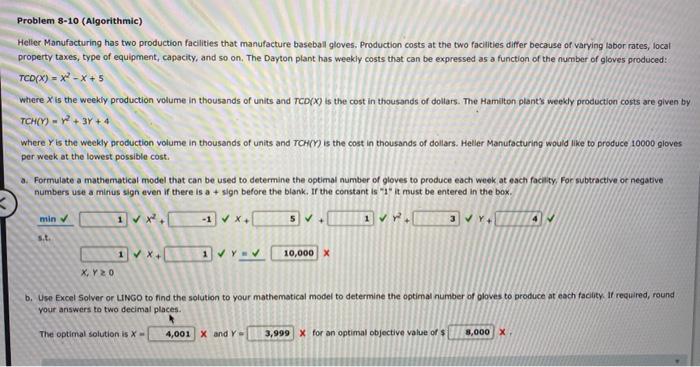
Problem 8-10 (Algorithmic) Heller Manufacturing has two production facilities that manufacture baseball gloves. Production costs at the two facilities differ because of varying labor rates, local property taxes, type of equipment, capacity, and so on. The Dayton plant has weekly costs that can be expressed as a function of the number of gloves produced TCDX) = XX+5 where X is the weekly production volume in thousands of units and TCD(X) is the cost in thousands of dollars. The Hamilton plant's weekly production costs are glven by TCH/Y) = 7+3+ 4 where is the weekly production volume in thousands of units and TCH() is the cost in thousands of dollars. Heller Manufacturing would like to produce 10000 gloves per week at the lowest possible cost. aFormulate a mathematical model that can be used to determine the optimal number of gloves to produce each week at each facility. For subtractive or negative numbers use a minus sign even if there is a sign before the blank. If the constant is "1" it must be entered in the box. -1 5 1 3 1 10,000 X X, Y20 b. Use Excel Solver or LINGO to find the solution to your mathematical model to determine the optimal number of gloves to produce at cach facility. If required, round your answers to two decimal places The optimal solution is X 4,001 X and Y - 3,999 X for an optimal objective value of $ 8,000 X mpter 08 Nonlinear Optimization Problem 8-10 (Algorithmic) Heller Manufacturing has two production facilities that manufacture baseball gloves. Production costs at the two facilitles differ because of varying labor rates, local property taxes, type of equipment, capacity, and so on. The Dayton plant has weekly costs that can be expressed as a function of the number of gloves produced: TCD(X) = x2-x+ 5 where X is the weekly production volume in thousands of units and TCD(X) is the cost in thousands of dollars. The Hamilton plant's weekly production costs are given by TCH(Y) - W+3Y+ 4 where Y is the weekly production volume in thousands of units and TCH(Y) is the cost in thousands of dollars. Heller Manufacturing would like to produce 10000 gloves per week at the lowest possible cost, a. Formulate a mathematical model that can be used to determine the optimal number of gloves to produce each week at each facility. For subtractive or negative numbers use a minus sign even if there is a + sign before the blank. If the constant is "1" it must be entered in the box. min -1 X+ 5 + 5.L. 1 X 10,000 X X, Y20 b. Use Excel Solver or LINGO to find the solution to your mathematical model to determine the optimal number of gloves to produce at each facility. W required, round your answers to two decimal places 8,000 X The optimal solution is X- 4,001 X and Y 3,999 X for an optimal objective value of Problem 8-10 (Algorithmic) Helier Manufacturing has two production facilities that manufacture baseball gloves. Production costs at the two facilities differ because of varying labor rates, local property taxes, type of equipment, capacity, and so on. The Dayton plant has weekly costs that can be expressed as a function of the number of gloves produced: TCD(X) = x -x + 5 where X is the weekly production volume in thousands of units and TCD(X) is the cost in thousands of dollars. The Hamilton plant's weekly production costs are given by TCH(Y) - 2 + 3y + 4 where is the weekly production volume in thousands of units and TCH() is the cost in thousands of dollars. Heller Manufacturing would like to produce 10000 gloves per week at the lowest possible cost. a. Formulate a mathematical model that can be used to determine the optimal number of gloves to produce each week at each facility. For subtractive or negative numbers use a minus sign even if there is a sign before the blank. Ir the constant is "1" it must be entered in the box. min 5 17 3 Y st 10,000 X X Y 20 b. Use Excel Solver or UINGO to find the solution to your mathematical model to determine the optimal number of loves to produce at each facility. If required, round your answers to two decimal places The optimal solution is X 4,001 X and Y 3,999 X for an optimal objective value of $ 8,000 X