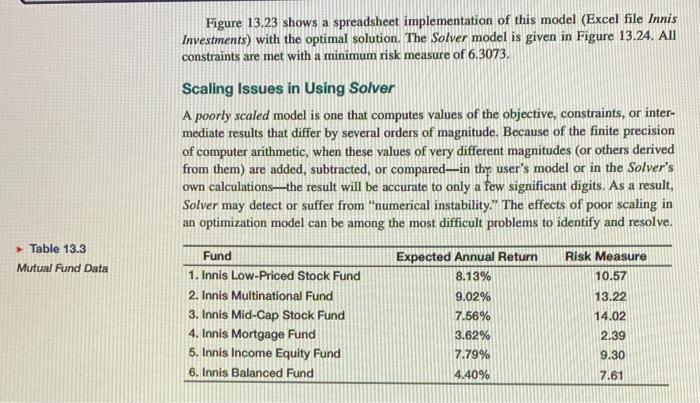
3. Review the portfolio allocation model in this chapter. Identify the decision variables, objective function, and constraints in simple verbal statements, and math- ematically formulate the linear optimization model. Chapter 13 Linear Optimization 495 EXAMPLE 13.16 Innis Investments Innis Investments is a small, family-owned business that manages personal financial portfolios. The company manages six mutual funds and has a client who has acquired $500,000 from an inheritance. Characteristics of the funds are given in Table 13.3. Innis Investments uses a proprietary algorithm to establish a measure of risk for its funds based on the historical volatility of the investments. The higher the volatility, the greater the risk. The company recommends that no more than $200,000 be invested in any individual fund, that at least $50,000 be invested in each of the multinational and balanced funds, and that the total amount invested in income equity and balanced funds be at least 40% of the total investment, or $200,000. The client would like to have an average return of at least 5% but would like to minimize risk. What portfolio would achieve this? Let X through Xe represent the dollar amount invested in funds 1 through 6, respectively. The total risk would be measured by the weighted risk of the portfolio, where the weights are the proportion of the total investment in any fund (X/500,000). Thus, the objective function is Minimize Total Risk = 10.57X+13.22X2 + 14.02X3 + 2.39X+9.30X5 +7.61X6 500,000 I The first constraint ensures that $500,000 is invested: X+X+X+X+X5+ X6 500,000 The next constraint ensures that the weighted return is at least 5%: 8.13X1+9.02X2+7.56X+3.62X4+7.79X+4.40X6 500,000 5.00 The next constraint ensures that at least 40% be invested in the income equity and balanced funds: Xs+X 0.4(500,000) The following constraints specify that at least $50,000 be invested in each of the multinational and balanced funds: X 2 50,000 X650,000 Finally, we restrict each investment to a maximum of $200,000 and include nonnegativity: X200,000 for/-1..... 6 X0 for 1..... 6 Table 13.3 Mutual Fund Data Figure 13.23 shows a spreadsheet implementation of this model (Excel file Innis Investments) with the optimal solution. The Solver model is given in Figure 13.24. All constraints are met with a minimum risk measure of 6.3073. Scaling Issues in Using Solver A poorly scaled model is one that computes values of the objective, constraints, or inter- mediate results that differ by several orders of magnitude. Because of the finite precision of computer arithmetic, when these values of very different magnitudes (or others derived from them) are added, subtracted, or compared-in the user's model or in the Solver's own calculations-the result will be accurate to only a few significant digits. As a result, Solver may detect or suffer from "numerical instability." The effects of poor scaling in an optimization model can be among the most difficult problems to identify and resolve. Fund 1. Innis Low-Priced Stock Fund 2. Innis Multinational Fund Expected Annual Return Risk Measure 8.13% 10.57 9.02% 13.22 3. Innis Mid-Cap Stock Fund 7.56% 14.02 4. Innis Mortgage Fund 3.62% 2.39 5. Innis Income Equity Fund 7.79% 9.30 6. Innis Balanced Fund 4.40% 7.61 G Clipboard A - Font % Conditional Formatting Format as Table Alignment Number Cell Styles Cells Editing Analyze Data A15 : x vfx A B C D E F G H 1 Portfolio Allocation Model 2 Note: this refers to the Innis Investments example, which was not clearly stated in the problem. Page 495 3 4 Decision Variables: 5 Objective: 6 Constraints: 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 M 1 22 23 24 25 126 727 28 29 30 31 32 33 34 D Ready + 13.2 13.3 13.5 13.11 + 100%