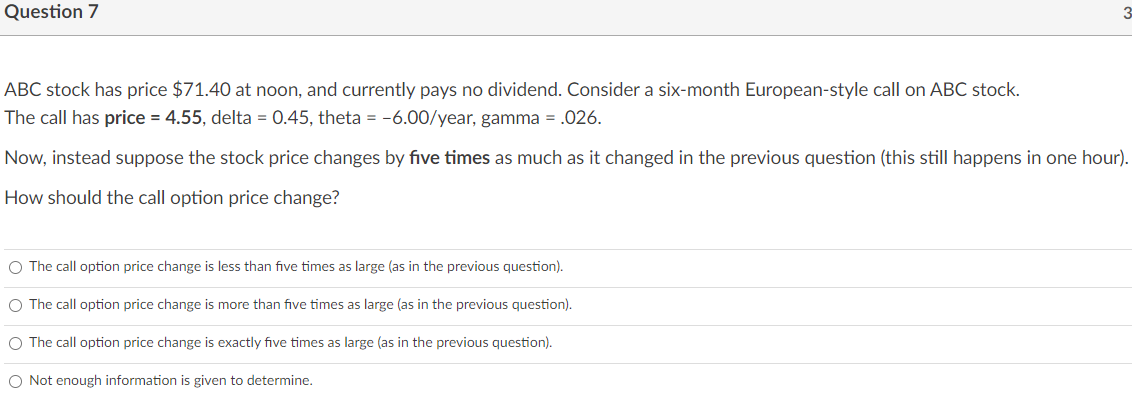
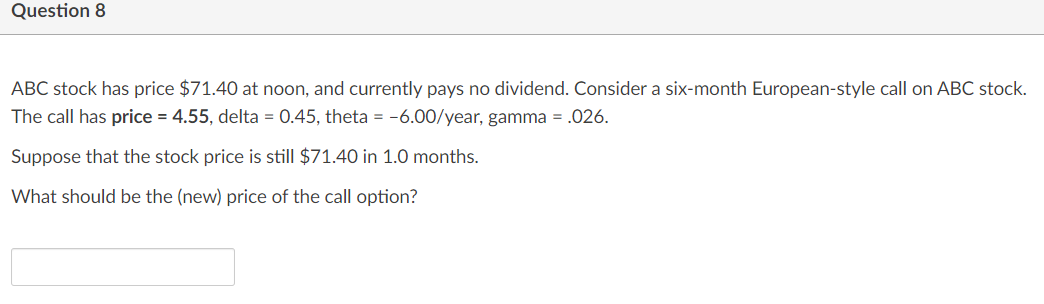
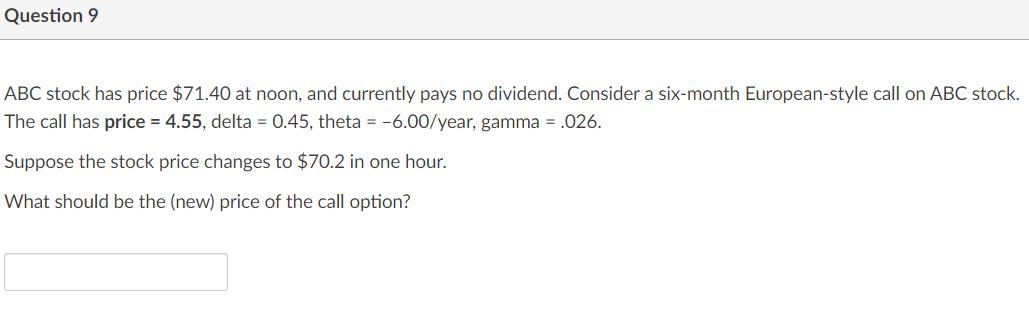
Question: Please help question 6-14 Question 10 ABC stock has price $71.40 at noon, and currently pays no dividend. There is a three-month European-style call on
Please help question 6-14
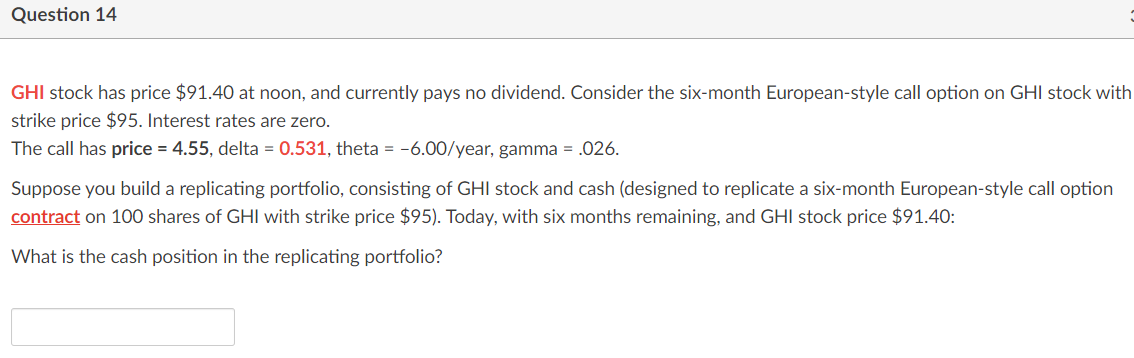
Question 10 ABC stock has price $71.40 at noon, and currently pays no dividend. There is a three-month European-style call on ABC stock with strike price $70. Interest rates are zero. This call has price = 5.00, delta = 0.58, theta = -8.35/year, gamma = .037. Consider the three-month European-style put option on ABC stock which (also) has strike price $70. What is the (fair) put price?Question 11 ABC stock has price $71.40 at noon, and currently pays no dividend. There is a three-month European-style call on ABC stock with strike price $70. Interest rates are zero. This call has price = 5.00, delta = 0.58, theta = -8.35/year, gamma = .037, vega = 14.0, and implied (annualized) stock volatility 30%. Consider the three-month European-style put option on ABC stock with strike price $35. Which of the following is the most likely implied stock volatility, derived from the three-month put option price? O 30% O 20% O 40% O All volatilities given (in the other answers) are equally likely.Question 12 3 | ABC stock has price $71.40 at noon, and currently pays no dividend. There is a three-month European-style call on ABC stock with strike price $70. Interest rates are zero. This call has price = 5.00, delta = 0.58, theta = 8.35/year, gamma = .037, vega = 14.0, and implied {annualized} stock volatility 30%. Suppose that you believe that (in contrast to the rest of the ma rket), over the next six months, the stock will have (annualized) volatility 45% (Assuming that you are correct} what is the call option actually worth today (with six months of option life remaining]? Question 13 a DEF stock has price $81.40 at noon, and currently pays no dividend. Consider the six-month European-style call option on DEF stock with strike price $85. Interest rates are zero. The call has price = 4.55, delta = 0.468, theta = 6.00Xyear, gamma = .026. Suppose you build a replicating portfolio, consisting of DEF stock and cash (designed to replicate a six-month European-style call option contract on 100 shares of DEF with strike price $85]. Today, with six months remaining. and DEF stock price $81.40: How many shares (of DEF) are in the replicating portfolio? Question 14 GHI stock has price $91.40 at noon, and currently pays no dividend. Consider the six-month European-style call option on GHI stock with strike price $95. Interest rates are zero. The call has price = 4.55, delta = 0.531, theta = -6.00/year, gamma = .026. Suppose you build a replicating portfolio, consisting of GHI stock and cash (designed to replicate a six-month European-style call option contract on 100 shares of GHI with strike price $95). Today, with six months remaining, and GHI stock price $91.40: What is the cash position in the replicating portfolio?Part II. Greeks. Questions 6-14. ABC stock has price $71.40 at noon, and currently pays no dividend. Consider a six-month European-style call on ABC stock. The call has price = 4.55, delta = 0.45, theta = 6.00/year, gamma = .026. Suppose the stock price changes to $72.5 in one hour. What should be the (new) price of the call option? Question 7 ABC stock has price $71.40 at noon, and currently pays no dividend. Consider a six-month European-style call on ABC stock. The call has price = 4.55, delta = 0.45, theta = -6.00/year, gamma = .026. Now, instead suppose the stock price changes by five times as much as it changed in the previous question (this still happens in one hour). How should the call option price change? The call option price change is less than five times as large (as in the previous question). O The call option price change is more than five times as large (as in the previous question). O The call option price change is exactly five times as large (as in the previous question). O Not enough information is given to determine.Question 8 ABC stock has price $71.40 at noon, and currently pays no dividend. Consider a six-month European-style call on ABC stock. The call has price = 4.55, delta = 0.45, theta = 6.00/year, gamma = .026. Suppose that the stock price is still $71.40 in 1.0 months. What should be the (new) price of the call option? Question 9 ABC stock has price $71.40 at noon, and currently pays no dividend. Consider a six-month European-style call on ABC stock. The call has price = 4.55, delta = 0.45, theta = 6.00fyear, gamma = .026. Suppose the stock price changes to $70.2 in one hour. What should be the (new) price of the call option