Please help, questions are as follows:

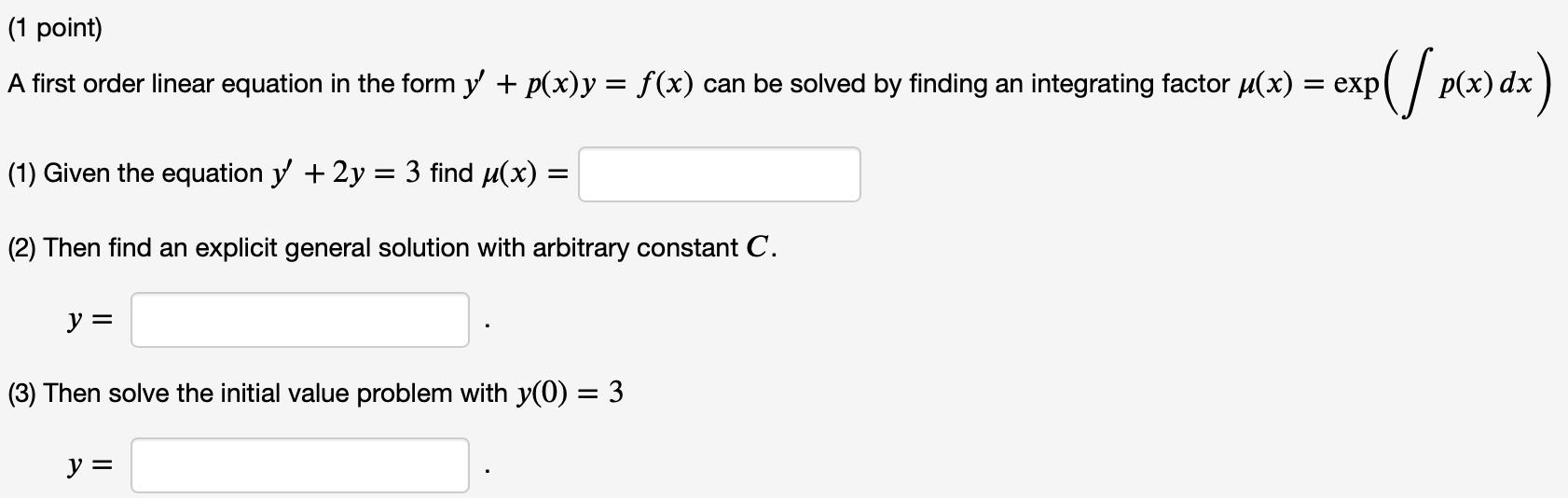
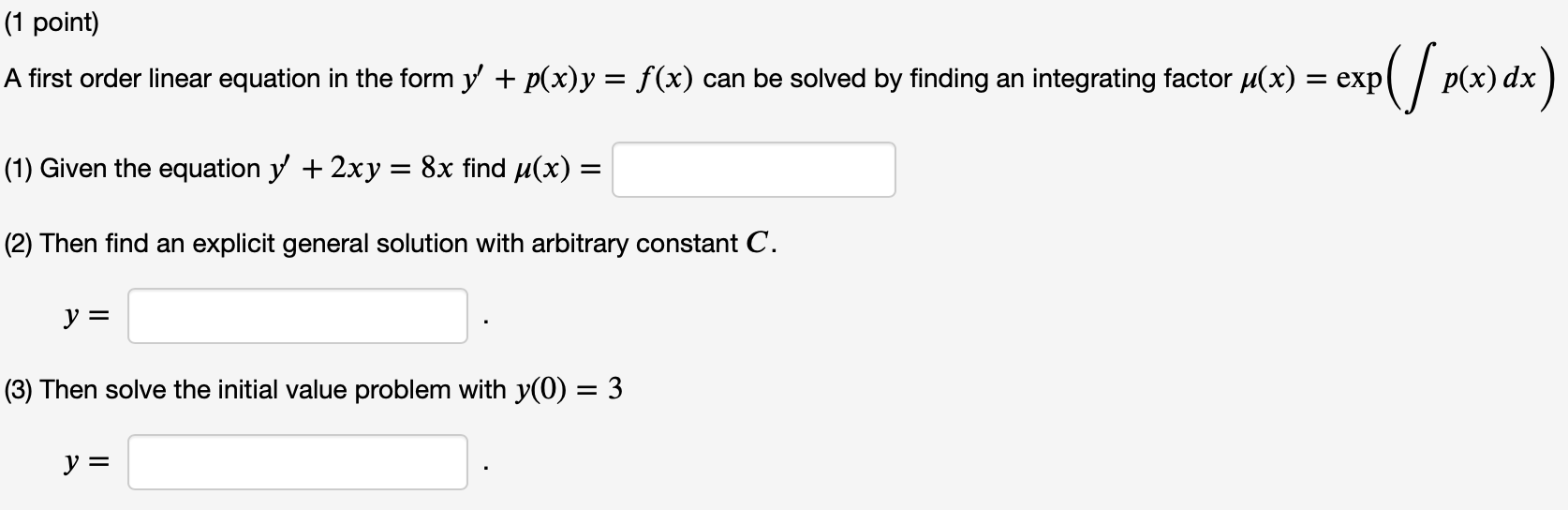
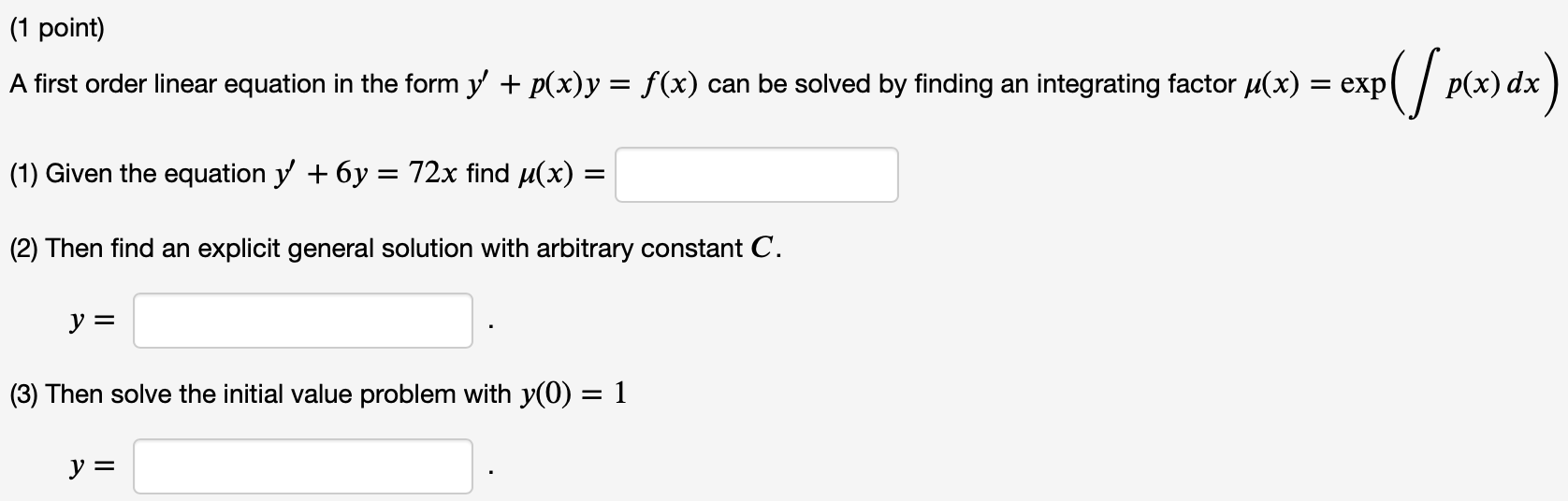
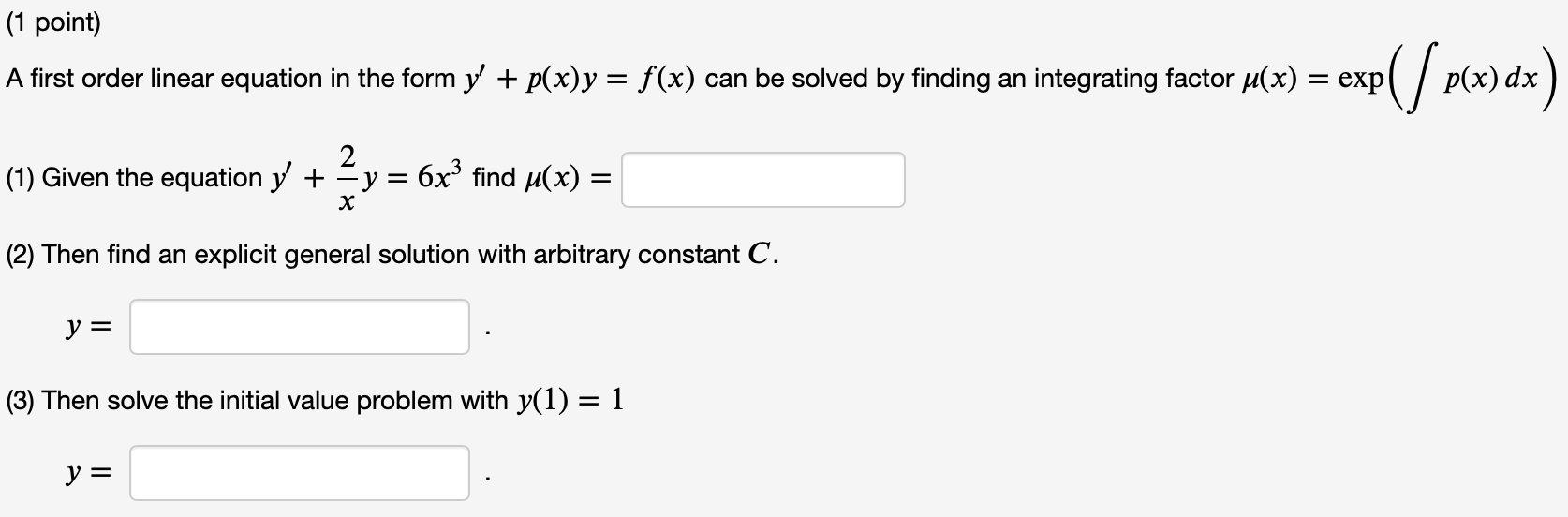
(1 point) A first order linear equation in the form y' + p(x)y = f (x) can be solved by finding an integrating factor ,u(x) = exp (/p(x) dx) (1) Given the equation )/ + 2y = 3 find \"(x) = (2) Then find an explicit general solution with arbitrary constant C. y = (3) Then solve the initial value problem with y(()) = 3 y: (1 point) A first order linear equation in the form y' + p(x)y = f(x) can be solved by finding an integrating factor \"(x) = exp (/ p(x) dx) (1) Given the equation 3/ + 2xy = 8x find \"(x) = (2) Then find an explicit general solution with arbitrary constant C. y = (3) Then solve the initial value problem with y(0) = 3 y: (1 point) A first order linear equation in the form 1/ + p(x)y = f (x) can be solved by finding an integrating factor \"(x) = exp (/ p(x) dx) (1) Given the equation y + 6y = 72x find \"(x) = (2) Then find an explicit general solution with arbitrary constant C. y = (3) Then solve the initial value problem with y(0) = 1 y: (1 point) A first order linear equation in the form y' + p(x)y = f (x) can be solved by finding an integrating factor u(x) = exp (/ p(x) dx) . . 2 3 . (1) Given the equation y' + y = 6x find ,u(x) = x (2) Then find an explicit general solution with arbitrary constant C. y = (3) Then solve the initial value problem with y(1) = 1 y