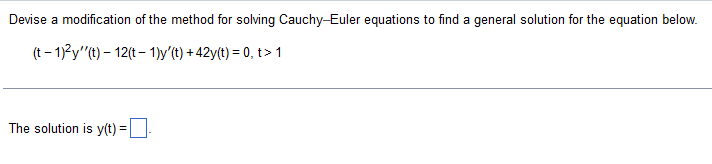
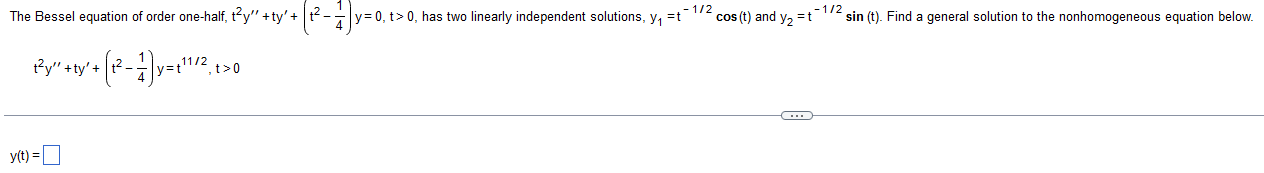
Please help! Thank you for your time tonight and no need to rush, take all the time you need!

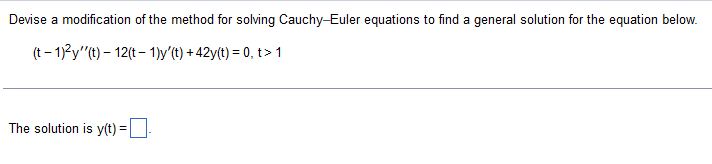
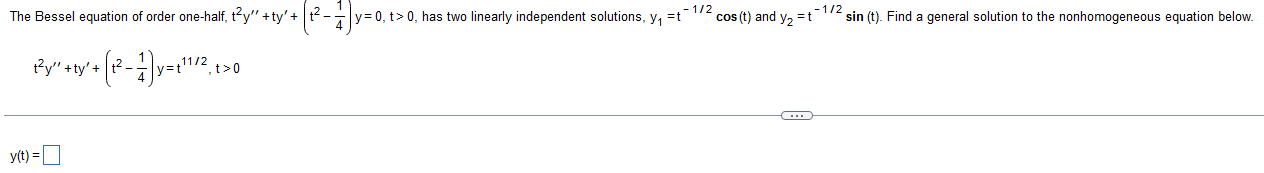
Devise a modification of the method for solving Cauchy-Euler equations to find a general solution for the equation below. (t - 1)2y"(t) - 12(t - 1)y'(t) + 42y(t) = 0, t> 1 The solution is y(t) =The Bessel equation of order one-half, try" + ty'+ t- - y=0, t> 0, has two linearly independent solutions, y, =t cos (t) and y, =tsin (t). Find a general solution to the nonhomogeneous equation below. thy " + ty' + ( 12 - _ y= + 1 1 12 , + 20 y(1) =_A differential equation and a nontrivial solution f are given below. Find a second linearly independent solution using reduction of order. Assume that all constants of integration are zero. tx" -(t + 1)x' + x=0, t> 0; f(t)= 3et X2(1) =