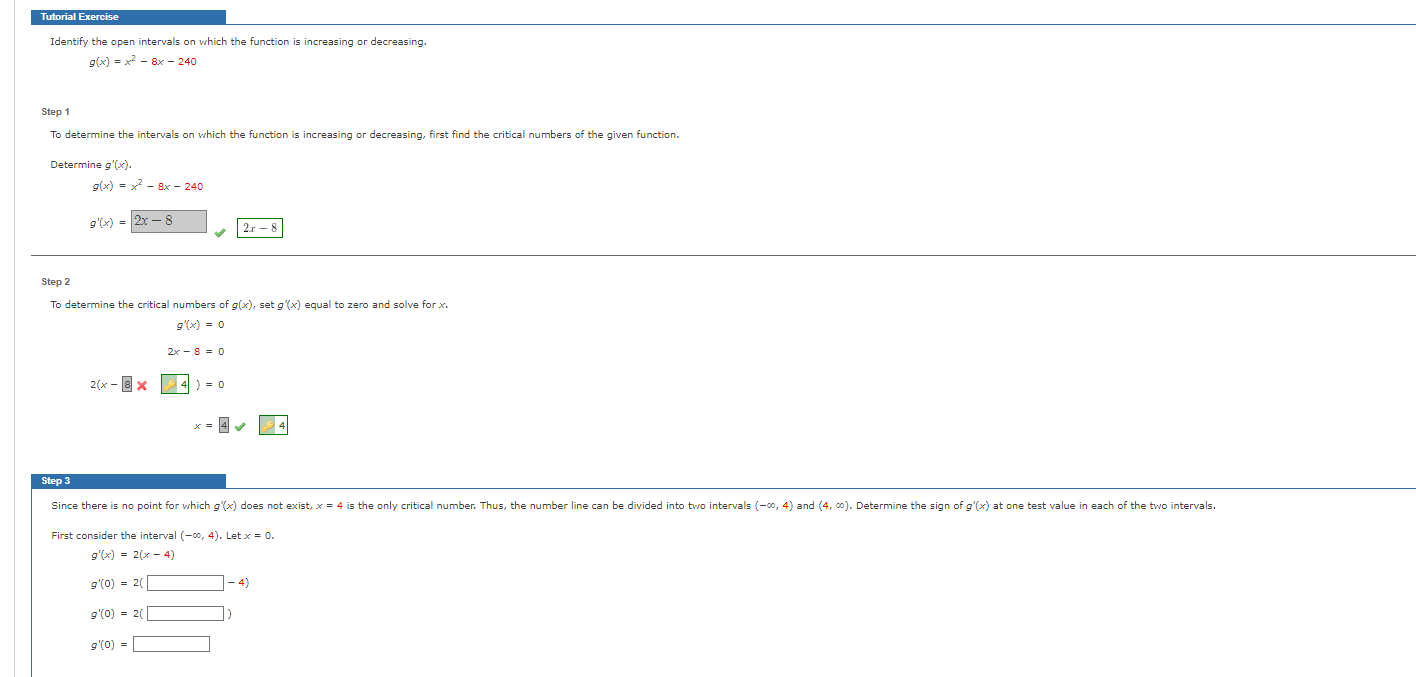
Please help with step 3

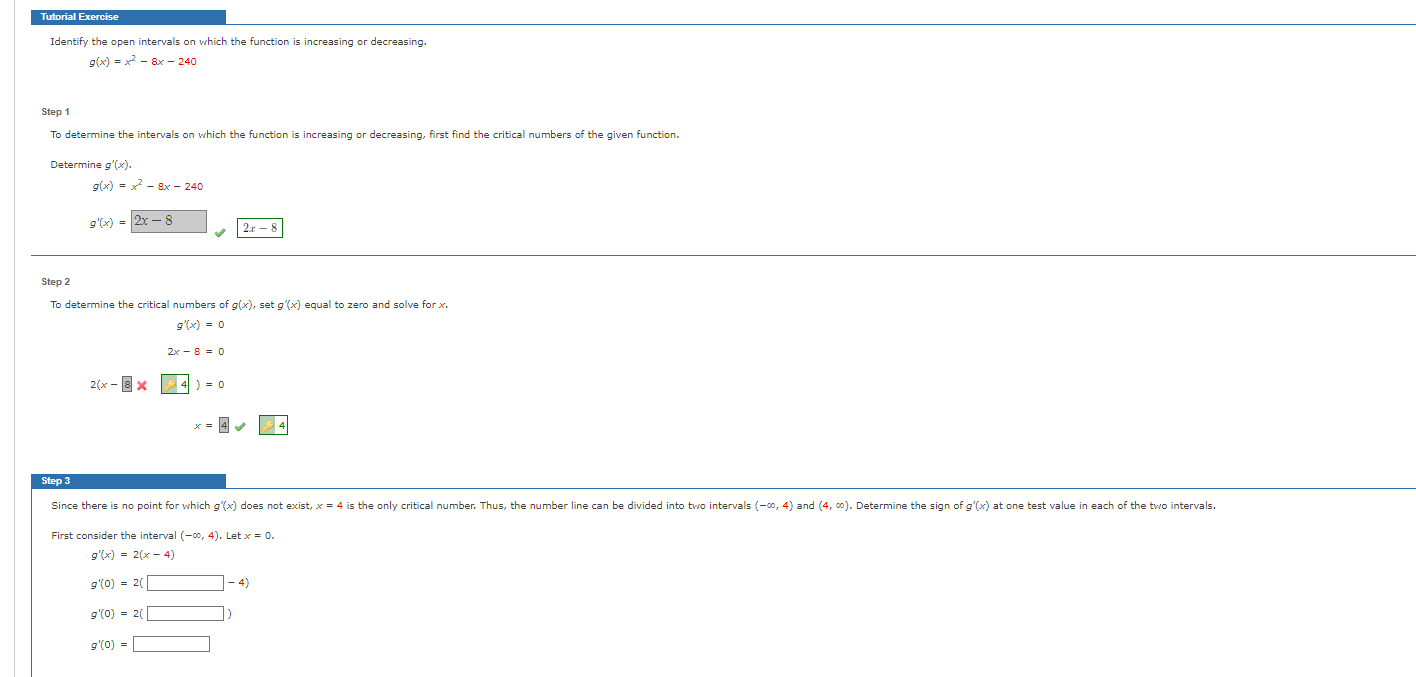
Tutorial Exercise Identify the open intervals on which the function is increasing or decreasing. g(x) = x2 - 8x - 240 Step 1 To determine the intervals on which the function is increasing or decreasing, first find the critical numbers of the given function. Determine g'(x). g(x) = x - 8x - 240 9'(x) = 2x - 8 2x - 8 Step 2 To determine the critical numbers of g(x), set g'(x) equal to zero and solve for x. 9 ( x) = 0 2x - 8 = 0 2(x - 8 X $ 4 ) =0 * = 4 0 $4 Step 3 Since there is no point for which g'(x) does not exist, x = 4 is the only critical number. Thus, the number line can be divided into two intervals (-00, 4) and (4, co). Determine the sign of g'(x) at one test value in each of the two intervals. First consider the interval (-00, 4). Let x = 0. g'(x) = 2(x - 4) g'(0) = 2( 9'(0) = 2( 9'(0) =