please help with this simple function in MATLAB syntax

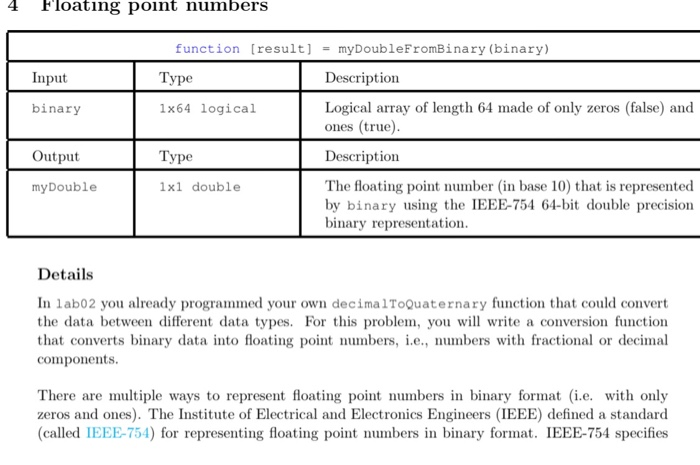
4 Floating point numbers function result] = myDoubleFromBinary (binary) Input Type Description binary 1x64 logical Logical array of length 64 made of only zeros (false) and ones (true) Output Type Description my Double 1x1 double The floating point number (in base 10) that is represented by binary using the IEEE-754 64-bit double precision binary representation. Details In labo2 you already programmed your own decimal ToQuaternary function that could convert the data between different data types. For this problem, you will write a conversion function that converts binary data into floating point numbers, i.e., numbers with fractional or decimal components. There are multiple ways to represent floating point numbers in binary format (i.e. with only zeros and ones). The Institute of Electrical and Electronics Engineers (IEEE) defined a standard (called IEEE-754) for representing floating point numbers in binary format. IEEE-754 specifies different formats, depending on how many bits (eg. 16 bits, 32 bits, 64 bits, 128 bits) are used to represent each floating point mumber. The formats that use 32 bits and 64 bits to represent each member are commonly known as "single precision and double precision", respectively. In MATLAB, you can experiment by defining a variable a that contains the value 1 (a - 1;) in the command window and then using the function whos to inspect the variables currently defined in the workspace. You should see that the class of variable a is double" and that it occupies 8 bytes = 64 bits of memory. Here is a figure showing the components of a double floating number in IEEE-754 e (11 bits) f(52 bits) 1 1 1 0 - 0 1 0 0 0 1 - 100 In this problem, we will consider double precision representations, where each number is repre sented using 64 bits (ie, a sequence of 64 zeros (false) and/or ones (true)). You will write a function to convert this logical array to its double floating point equivalent. We index the bits from left to right: the left-most bit is the 1s* bit and the right-most bit is the 64th bit. Instead of utilizing each bit as the coefficient of a power of 2, floats allocate bits to three different parts: the sign indicator, s, which says whether a number is positive or negative; characteristic or exponent, e, which is the power of 2; and the fraction, f, which is the coefficient of the exponent. To be more specifie, the number represented by a sequence of 64 bits can be calculated using the following formula: n = (-1)".20-1025. (1+ where n represents the decimal format of the floating mumber. For example: 001111111111 01000000000000000000000000000000000000000000000000000. Its exponent decimal is e = 1-2 +1-21 +1-22 +1-23 +1-24 +1-23 +1-4 +1-27 +1-29 +1 -2 = 1023 f=1 (-1)21023-1023 - (1 +0.25) = 1.25 However, there are special cases where the above formula does not necessarily apply. Remember to program these cases into your function. ife = 0 and 5 +0, n=(-1)* 2-1023. (1+) . ife = 0 and f = 0, n=0 ife = 2017 and f = 0, n= (-1) ife = 2047 and 0, n = NaN(Not a Number) 4 Floating point numbers function result] = myDoubleFromBinary (binary) Input Type Description binary 1x64 logical Logical array of length 64 made of only zeros (false) and ones (true) Output Type Description my Double 1x1 double The floating point number (in base 10) that is represented by binary using the IEEE-754 64-bit double precision binary representation. Details In labo2 you already programmed your own decimal ToQuaternary function that could convert the data between different data types. For this problem, you will write a conversion function that converts binary data into floating point numbers, i.e., numbers with fractional or decimal components. There are multiple ways to represent floating point numbers in binary format (i.e. with only zeros and ones). The Institute of Electrical and Electronics Engineers (IEEE) defined a standard (called IEEE-754) for representing floating point numbers in binary format. IEEE-754 specifies different formats, depending on how many bits (eg. 16 bits, 32 bits, 64 bits, 128 bits) are used to represent each floating point mumber. The formats that use 32 bits and 64 bits to represent each member are commonly known as "single precision and double precision", respectively. In MATLAB, you can experiment by defining a variable a that contains the value 1 (a - 1;) in the command window and then using the function whos to inspect the variables currently defined in the workspace. You should see that the class of variable a is double" and that it occupies 8 bytes = 64 bits of memory. Here is a figure showing the components of a double floating number in IEEE-754 e (11 bits) f(52 bits) 1 1 1 0 - 0 1 0 0 0 1 - 100 In this problem, we will consider double precision representations, where each number is repre sented using 64 bits (ie, a sequence of 64 zeros (false) and/or ones (true)). You will write a function to convert this logical array to its double floating point equivalent. We index the bits from left to right: the left-most bit is the 1s* bit and the right-most bit is the 64th bit. Instead of utilizing each bit as the coefficient of a power of 2, floats allocate bits to three different parts: the sign indicator, s, which says whether a number is positive or negative; characteristic or exponent, e, which is the power of 2; and the fraction, f, which is the coefficient of the exponent. To be more specifie, the number represented by a sequence of 64 bits can be calculated using the following formula: n = (-1)".20-1025. (1+ where n represents the decimal format of the floating mumber. For example: 001111111111 01000000000000000000000000000000000000000000000000000. Its exponent decimal is e = 1-2 +1-21 +1-22 +1-23 +1-24 +1-23 +1-4 +1-27 +1-29 +1 -2 = 1023 f=1 (-1)21023-1023 - (1 +0.25) = 1.25 However, there are special cases where the above formula does not necessarily apply. Remember to program these cases into your function. ife = 0 and 5 +0, n=(-1)* 2-1023. (1+) . ife = 0 and f = 0, n=0 ife = 2017 and f = 0, n= (-1) ife = 2047 and 0, n = NaN(Not a Number)