Please I need help with this Matlab code for the convolution shown in Section 2. Ignore the question part that makes reference to Section 1.

However I did include an example M3.4.

I still would like to see what the code looks like in Matlab or text file, with the plot included.

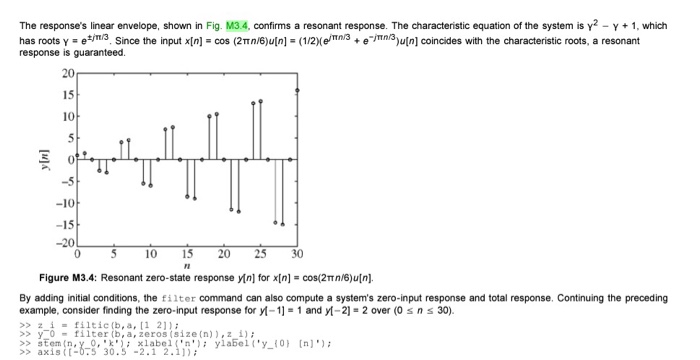
The response's linear envelope, shown in Fig. M3.4, confirms a resonant response. The characteristic equation of the system is y2 1, which has roots Y-et/m . Since the input x n = cos (2??/6)u n = (1/2 em 3 + e-mn/3)u(n] coincides with the characteristic roots a resonant 20 15 10 -10 -15 -20 0 5 10 5 20 25 30 Figure M3.4: Resonant zero-state response in] for xIn] cos(2TTn/6)u[n] By adding initial conditions, the filter command can also compute a system's zero-input response and total response. Continuing the preceding example, consider finding the zero-input response for y11 and y-2 2 over (0 sns 30). >> y-o-filter (b,a,zeros ( size(n)),2 ); >> stem (n,y0,xlabel 'n' ylabel('y 0) [n' >> axis(t-075 30.5-2.1 2.11)