Please include R code is possible

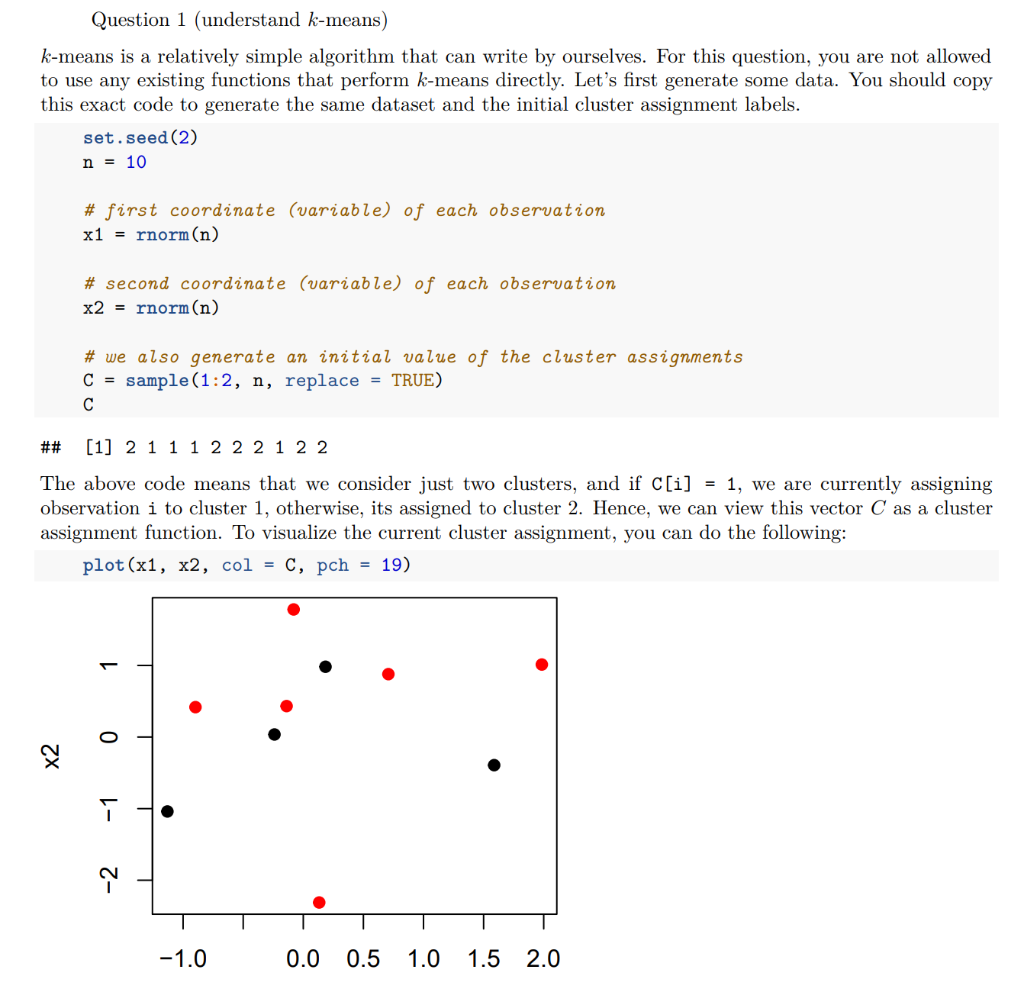
Question 1 (understand k-means) k-means is a relatively simple algorithm that can write by ourselves. For this question, you are not allowed to use any existing functions that perform k-means directly. Let's first generate some data. You should copy this exact code to generate the same dataset and the initial cluster assignment labels set.seed (2) n - 10 # first coordinate (uam able) of each observation x1 - rnorm(n) # second coordinate (variable) of each obser ation x2 = rnorm (n) # we also generate an initial value of the cluster assignments C sample (1:2, n, replace TRUE) ## [1] 2 1 1 1 2 2 2 1 2 2 The above code means that we consider just two clusters, and if C[1] = 1, we are currently assigning observation i to cluster 1, otherwise, its assigned to cluster 2. Hence, we can view this vector C as a cluster assignment function. To visualize the current cluster assignment, you can do the following: plot (x1, x2, col = C, pch- 19) 0.0 0.5 1.0 1.5 2.0 We know that in each iteration of the k-means algorithm, we first fix the cluster assignment function and update the cluster means mk, for k = 1,K. then, fix the cluster means and update the cluster assignment function a. [2 points] Do this iteration once, and output the new cluster assignment function (both the value of the vector C and plot it) and the cluster means for both clusters b. [2 points] Write the above two steps into a single function. Repeatedly call this function to update C and the cluster means. When they do not change anymore, stop the algorithm. You should not have an c.[2 points] Based on your final result, calculate and report the within-cluster distance of the k-mearn d. [2 points] Randomly generate another set of initial values for C and repeat the above steps. Observe if e. [2 points] Apply any clustering algorithm discussed in the lecture other than k-means on the same data excessively long output for this part. Only output the final result. algorithm, which is also the objective function used for k-means. the two runs lead to the same clustering result. Comment on your findings. set. Compare the result by using this algorithm with what you got by using k-means Question 1 (understand k-means) k-means is a relatively simple algorithm that can write by ourselves. For this question, you are not allowed to use any existing functions that perform k-means directly. Let's first generate some data. You should copy this exact code to generate the same dataset and the initial cluster assignment labels set.seed (2) n - 10 # first coordinate (uam able) of each observation x1 - rnorm(n) # second coordinate (variable) of each obser ation x2 = rnorm (n) # we also generate an initial value of the cluster assignments C sample (1:2, n, replace TRUE) ## [1] 2 1 1 1 2 2 2 1 2 2 The above code means that we consider just two clusters, and if C[1] = 1, we are currently assigning observation i to cluster 1, otherwise, its assigned to cluster 2. Hence, we can view this vector C as a cluster assignment function. To visualize the current cluster assignment, you can do the following: plot (x1, x2, col = C, pch- 19) 0.0 0.5 1.0 1.5 2.0 We know that in each iteration of the k-means algorithm, we first fix the cluster assignment function and update the cluster means mk, for k = 1,K. then, fix the cluster means and update the cluster assignment function a. [2 points] Do this iteration once, and output the new cluster assignment function (both the value of the vector C and plot it) and the cluster means for both clusters b. [2 points] Write the above two steps into a single function. Repeatedly call this function to update C and the cluster means. When they do not change anymore, stop the algorithm. You should not have an c.[2 points] Based on your final result, calculate and report the within-cluster distance of the k-mearn d. [2 points] Randomly generate another set of initial values for C and repeat the above steps. Observe if e. [2 points] Apply any clustering algorithm discussed in the lecture other than k-means on the same data excessively long output for this part. Only output the final result. algorithm, which is also the objective function used for k-means. the two runs lead to the same clustering result. Comment on your findings. set. Compare the result by using this algorithm with what you got by using k-means