Please include solver reports and recommendations and analysis

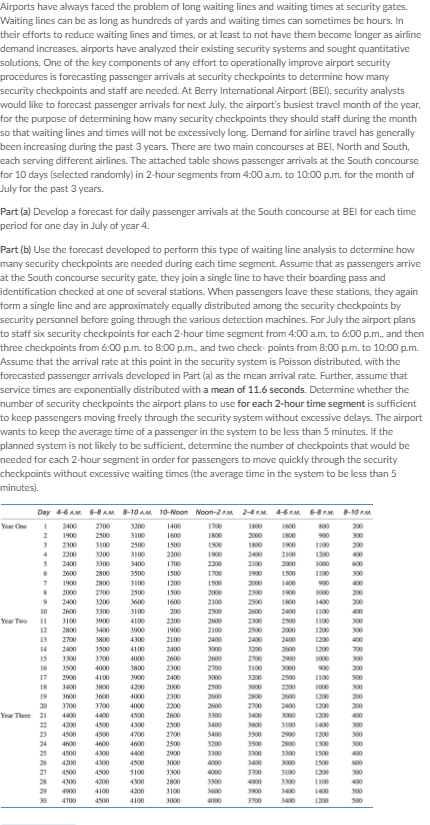
Airports have always faced the problem of long waiting lines and waiting times at security gates. Waiting lines can be as long as hundreds of yards and waiting times can sometimes be hours. In their efforts to reduce waiting lines and times, or at least to not have them become longer as airline demand increases, airports have analyzed their existing security systems and sought quantitative solutions. One of the key components of any effort to operationally improve airport security procedures is forecasting passenger arrivals at security checkpoints to determine how many security checkpoints and staff are needed. At Berry International Airport (BEI), security analysts would like to forecast passenger arrivals for next July, the airport's busiest travel month of the year, for the purpose of determining how many security checkpoints they should staff during the month so that waiting lines and times will not be excessively long. Demand for airline travel has generally been increasing during the past 3 years. There are two main concourses at BEI, North and South, each serving different airlines. The attached table shows passenger arrivals at the South concourse for 10 days (selected randomly) in 2-hour segments from 4:00 a.m. to 10:00 p.m. for the month of July for the past 3 years. Part (a) Develop a forecast for daily passenger arrivals at the South concourse at BEI for each time period for one day in July of year 4. Part (b) Use the forecast developed to perform this type of waiting line analysis to determine how many security checkpoints are needed during each time segment. Assume that as passengers arrive at the South concourse security gate, they join a single line to have their boarding pass and identification checked at one of several stations. When passengers leave these stations, they again form a single line and are approximately equally distributed among the security checkpoints by security personnel before going through the various detection machines. For July the airport plans to staff six security checkpoints for each 2-hour time segment from 4:00 a.m. to 6:00p.m., and then three checkpoints from 6:00 p.m. to 8:00p.m., and two check points from 8:00 p.m. to 10:00 p.m. Assume that the arrival rate at this point in the security system is Poisson distributed, with the forecasted passenger arrivals developed in Part (a) as the mean arrival rate. Further, assume that service times are exponentially distributed with a mean of 11.6 seconds. Determine whether the number of security checkpoints the airport plans to use for each 2-hour time segment is sufficient to keep passengers moving freely through the security system without excessive delays. The airport wants to keep the average time of a passenger in the system to be less than 5 minutes. If the planned system is not likely to be sufficient, determine the number of checkpoints that would be needed for each 2-hour segment in order for passengers to move quickly through the security checkpoints without excessive waiting times the average time in the system to be less than 5 minutes). Day 46 AM 8-10AM. 10-Noon Noon-2AM 24.1.4-6AM -8.8-10 AM Year 1 IND 1900 200 200 2000 2500 3100 3200 3300 4 $ 3100 2500 3100 3400 3500 3100 2500 3600 3100 1600 1500 2300 1700 1500 1200 2000 1900 1100 200 3400 2100 2000 200 1900 1500 1100 3000 1700 7 1900 2000 200 2700 3200 3300 2100 2500 200 1600 200 10 2500 100 100 2000 2000 1100 Year The 4100 2400 2600 3100 2800 2700 2400 1900 3400 3800 1300 2400 2000 2500 2000 200 2000 1200 2400 30 300 16 17 3500 2900 4000 4100 100 3600 3700 4400 9900 4300 4100 1000 3800 3900 4200 4000 4000 2300 2400 200 200 2200 400 700 200 200 Son 0 300 200 3000 19 20 Year These 21 5200 4400 4200 2700 3100 3000 300 2000 2200 2500 1100 23000 2300 2000 200 200 300 2600 2700300 200 3300 3000 1300 34000 310000 5000 3500 200 300 3200 3500 200 300 3300 3300 300 500 2700 ARRAXARXAR 25 100 4600 4500 4300 4900 4300 4900 4700 27 40 2500 4700 4600 2500 4400 2900 3000 5100 300 200 4200 3100 4100 3000 4600 40 4900 4500 4200 4100 4500 000 3700 3100 1300 3500 4000 3300 1100 200 400 500 500 4000 1200