Please make a Python program to solve Example 7 using the combined bisection - secant method. Reproduce Tables 7 and 8.

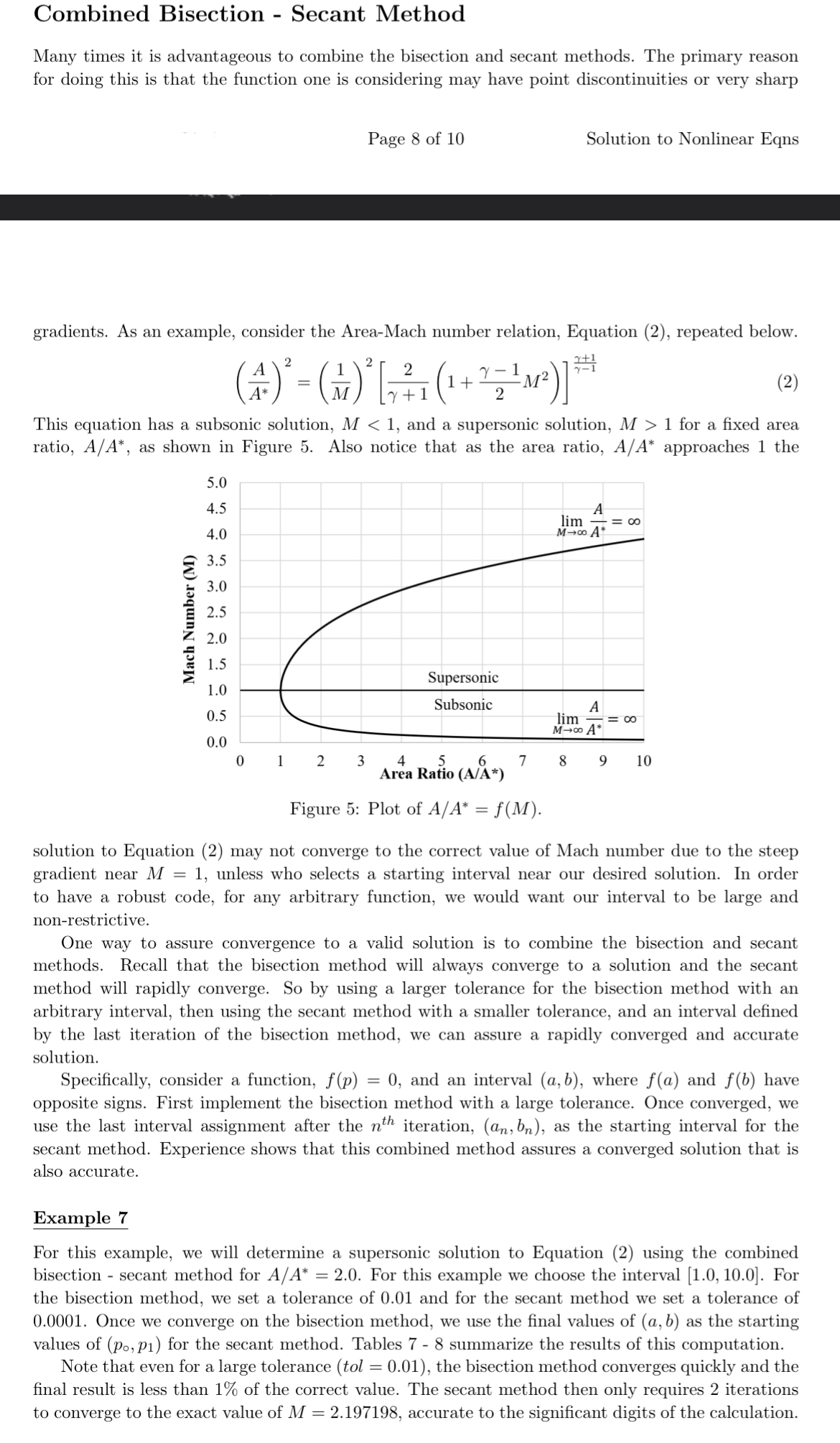
Combined Bisection - Secant Method Many times it is advantageous to combine the bisection and secant methods. The primary reason for doing this is that the function one is considering may have point discontinuities or very sharp gradients. As an example, consider the Area-Mach number relation, Equation (2), repeated below. 2+1 2 2 2 (4) = ( - ) [, ( + M)]* (1 Y- 2 Mach Number (M) (2) This equation has a subsonic solution, M < 1, and a supersonic solution, M> 1 for a fixed area ratio, A/A*, as shown in Figure 5. Also notice that as the area ratio, A/A* approaches 1 the 5.0 4.5 4.0 3.5 3.0 2.5 2.0 1.5 1.0 0.5 0.0 0 1 Page 8 of 10 2 3 Supersonic Subsonic Solution to Nonlinear Eqns 7 4 Area Ratio (A/A Figure 5: Plot of A/A* = f(M). A lim = 00 M00 A* A lim M0 A* 8 9 10 = solution to Equation (2) may not converge to the correct value of Mach number due to the steep gradient near M = 1, unless who selects a starting interval near our desired solution. In order to have a robust code, for any arbitrary function, we would want our interval to be large and non-restrictive. One way to assure convergence to a valid solution is to combine the bisection and secant methods. Recall that the bisection method will always converge to a solution and the secant method will rapidly converge. So by using a larger tolerance for the bisection method with an arbitrary interval, then using the secant method with a smaller tolerance, and an interval defined by the last iteration of the bisection method, we can assure a rapidly converged and accurate solution. Specifically, consider a function, f(p) = 0, and an interval (a, b), where f(a) and f(b) have opposite signs. First implement the bisection method with a large tolerance. Once converged, we use the last interval assignment after the nth iteration, (an, bn), as the starting interval for the secant method. Experience shows that this combined method assures a converged solution that is also accurate. Example 7 For this example, we will determine a supersonic solution to Equation (2) using the combined bisection - secant method for A/A* = 2.0. For this example we choose the interval [1.0, 10.0]. For the bisection method, we set a tolerance of 0.01 and for the secant method we set a tolerance of 0.0001. Once we converge on the bisection method, we use the final values of (a, b) as the starting values of (po, p1) for the secant method. Tables 7 - 8 summarize the results of this computation. Note that even for a large tolerance (tol = 0.01), the bisection method converges quickly and the final result is less than 1% of the correct value. The secant method then only requires 2 iterations to converge to the exact value of M = 2.197198, accurate to the significant digits of the calculation.