please match step with the property

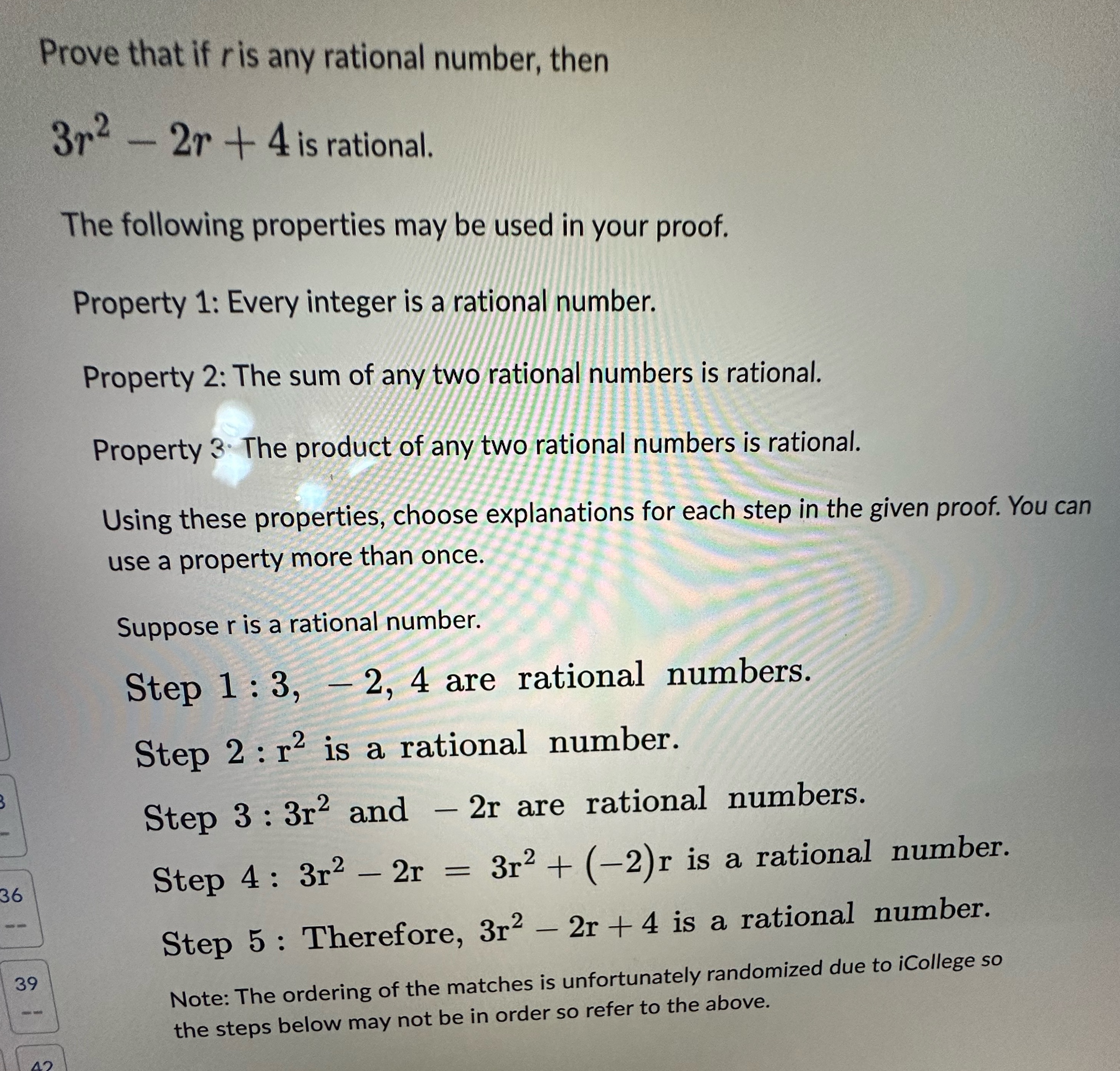
Prove that if ris any rational number, then 3r2 - 2r + 4 is rational. The following properties may be used in your proof. Property 1: Every integer is a rational number. Property 2: The sum of any two rational numbers is rational. Property 3: The product of any two rational numbers is rational. Using these properties, choose explanations for each step in the given proof. You can use a property more than once. Suppose r is a rational number. Step 1 : 3, - 2, 4 are rational numbers. Step 2: r2 is a rational number. Step 3 : 3r2 and - 2r are rational numbers. Step 4: 3r2 - 2r = 3r2 + (-2)r is a rational number. 36 Step 5 : Therefore, 3r2 - 2r + 4 is a rational number. 39 Note: The ordering of the matches is unfortunately randomized due to iCollege so the steps below may not be in order so refer to the above