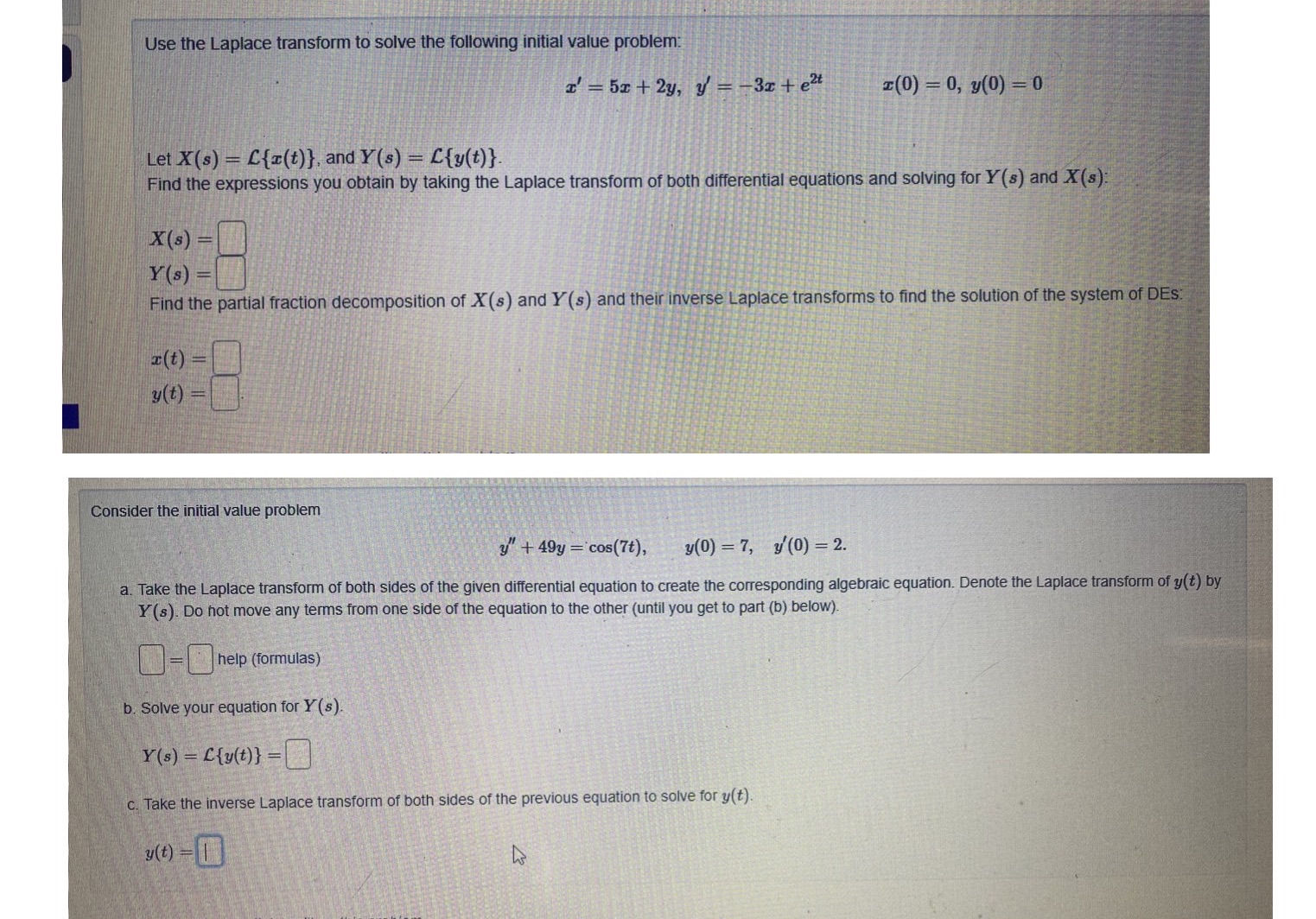
Question: Please need an answer asap Use the Laplace transform to solve the following initial value problem: I' = 5x + 2y, y' = -3x +

Please need an answer asap

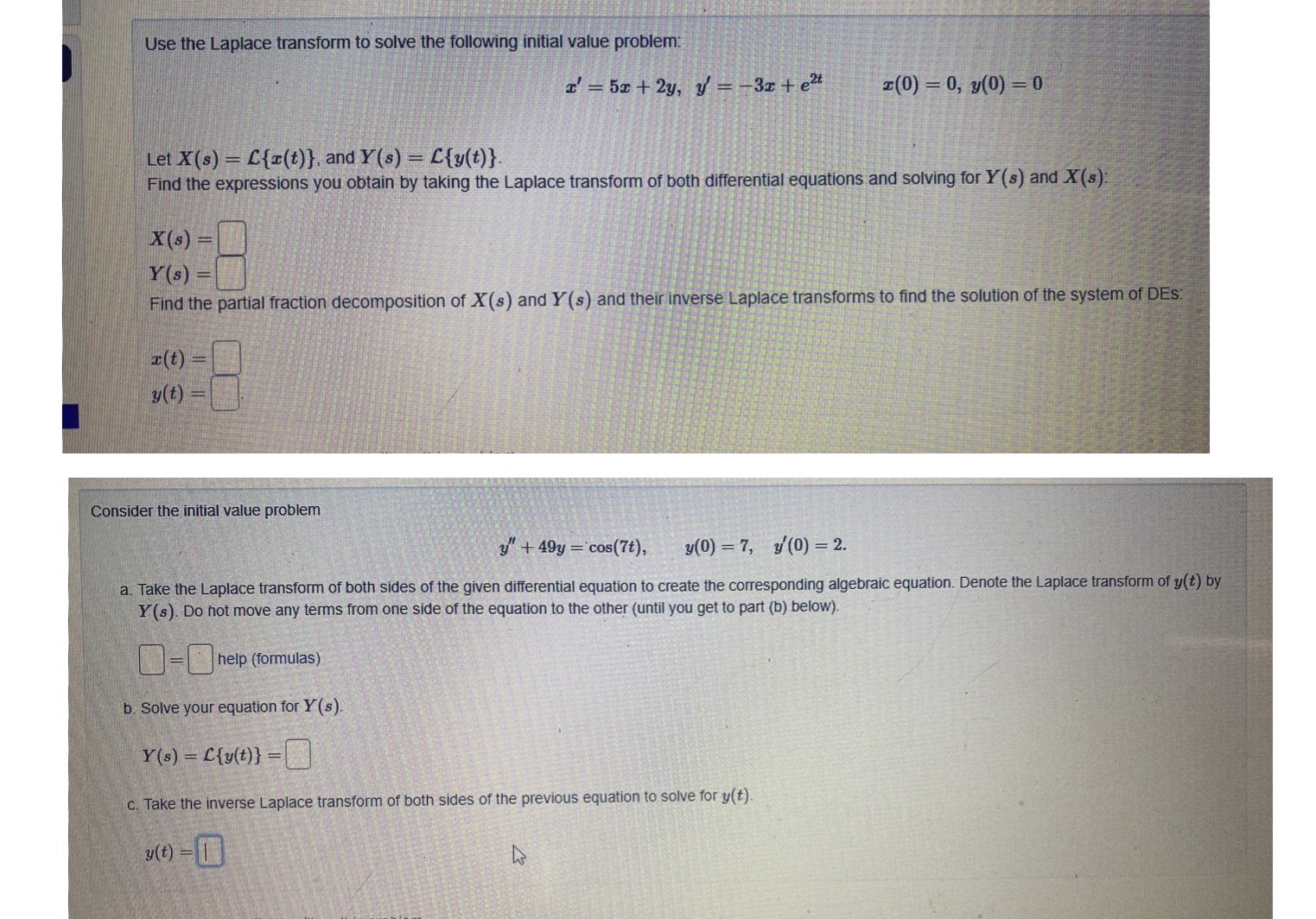
Use the Laplace transform to solve the following initial value problem: I' = 5x + 2y, y' = -3x + e2t I(0) = 0, y(0) = 0 Let X(s) = [{x(t) }, and Y(s) = Cty(t) } Find the expressions you obtain by taking the Laplace transform of both differential equations and solving for Y(s) and X(s) X(s) = Y(s) = Find the partial fraction decomposition of X(s) and Y (s) and their inverse Laplace transforms to find the solution of the system of DES. I(t) = y(t) Consider the initial value problem y" + 49y =cos(7t), y(0) =7, y'(0) = 2. a. Take the Laplace transform of both sides of the given differential equation to create the corresponding algebraic equation. Denote the Laplace transform of y(t) by Y (s). Do not move any terms from one side of the equation to the other (until you get to part (b) below). 0-help (formulas) b. Solve your equation for Y (s). Y(s) = [ly(t)} = c. Take the inverse Laplace transform of both sides of the previous equation to solve for y(t) y(t ) - 1

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Please need an answer asap Use the Laplace transform to solve the following initial value problem: 3 - 4y' + 20y = 0 y(0) = 0, y (0) = 4 a. Using Y for the Laplace transform of y(t), i.e., Y =...

Please need an answer asap Use the Laplace transform to solve the following initial value problem: 1/' - 47 + 4y = 0 3/(0) = -2, 1/(0) = 3 a. Using Y for the Laplace transform of y(t), i.e., Y =...

Please need an answer asap Use the Laplace transform to solve the following initial value problem: y" - 4y + 4y =0 y(0) = -2, y'(0) = 3 a. Using Y for the Laplace transform of y(t), i.e., Y =...

Please need an answer aspa Use the Laplace transform to solve the following initial value problem: y' + 2y' = 0 y(0) - 1, y'(0) = 4 a. Using Y for the Laplace transform of y(t), i.e., Y = [fy(t)},...

Please need an answer asap Use the Laplace transform to solve the following initial value problem: 3/" + 63/ - 27y = 0 y(0) = 4, 1/(0) =-1 a. First, using Y for the Laplace transform of y(t). i.e., Y...

Please need an answer asap Use the Laplace transform to solve the following initial value problem: y' - 23/ + 26y=0 y(0) = 0, y (0) =5 a. Using Y for the Laplace transform of y(t), i.e., Y = [ty(t)...

Please need an answer asap Use the Laplace transform to solve the following initial value problem: if' + Ay = cos(5t) #/(0) =0, 1/(0) -0 First, using Y for the Laplace transform of y(t), i.e., Y =...

Please need an answer asap Use the Laplace transform to solve the following initial value problem: y' - 27/ + 26y=0 y(0) = 0, y/(0) =5 a. Using Y for the Laplace transform of y(t), i.e., Y = [ty(t)...

Section 6.2 Solution of I.V.P: Problem 7 Previous Problem Problem List Next Problem (1 point) Use the Laplace transform to solve the following initial value problem: y' - 2y' + 26y = 0 y(0) = 0,...

Please need an answer asap Use the Laplace transform to solve the following initial value problem: y' + 4y = cos(5t) y(0) = 0, y(0) =0 First, using Y for the Laplace transform of y(t), i.e., Y =...

What is the cost of the ending inventory for FIFO and LIFO. A FIFO: Purchases Cost of Goods Sold Inventory Date Unit Cost Total Cost Unit Cost Total Cost of Goods Sold Total Cost Quantity Quantity...

The reaction 2NO (g) + 02 (g) 2NO2 (g) has the third-order rate law: rate = k[NO]2 [O2], where k = 25 M 's1. Under the condition that [NO] =2 [O2], 8kt + 1 the integrated rate law is What are the...

Companies may raise capital by issuing debt instruments, also known as: a debenture. bonds. promissory notes. common stock.

A hula hoop and solid disc of equal radii are rolled, from rest and without slipping, down an incline plane. Which one will reach the bottom of the inclined plane first? Explain.

At the annual shareholders" meeting, the president of the Lilly Coiporation made the following statement: "'The earnings for the year, after taxes, was $1,096,000. The directors have decided that the...

Distinguish between the nature of. and accounting for. a correction of an error in previously issued financial statements and the adjustment for a change in an accounting estimate made in preparing...

Distinguish among the following three terms: comprehensive income, other comprehensive income, and accumulated otiier comprehensive income. What would the term accumulated comprehensive income, not...