Please only use definitions, propositions, theorems given in the book ''Differential Topology'' by Guillemin and Pollack !

And if you refer to a proposition, theorem or exercise in the book please refer to them by chapter and section!

Also please explain each step, even if it seems trivial to you!

Please don't answer this question by using theory that is NOT covered in the book by Guillemin and Pollack!!!! The Propositions and Theorems in the book of Guillemin and Pollack are NOT numbered, so if you end up referring to Propositions by numbers, you are using the WRONG book!

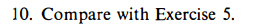
10. Let v be a vector field on R' with finitely many zeros, and suppose that the sum of the indices of its zeros is 0. Show that there exists a vector field that has no zeros, yet equals v outside a compact set.5. Let f: R* - R* be a smooth map with 0 as a regular value. Suppose that f-(0) is finite and that the number of preimage points in f-1(0) is zero when counted with the usual orientation convention. Assuming the special case in dimension k - 1, prove that there exists a mapping g : R* - R* - {0] such that g = f outside a compact set.10. Compare with Exercise 5