Please only use definitions, propositions, theorems given in the book ''Differential Topology'' by Guillemin and Pollack !

And if you refer to a proposition, theorem or exercise in the book please refer to them by chapter and section!

Also please explain each step, even if it seems trivial to you!

Please don't answer this question by using theory that is NOT covered in the book by Guillemin and Pollack!!!!

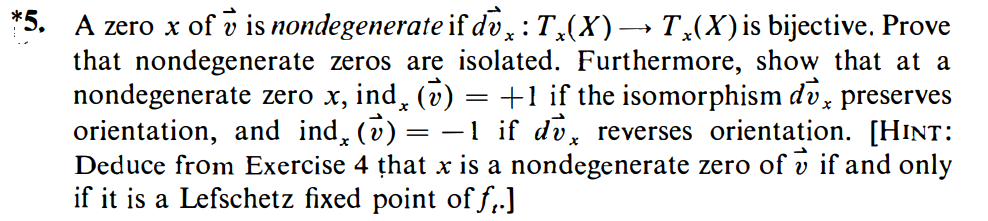
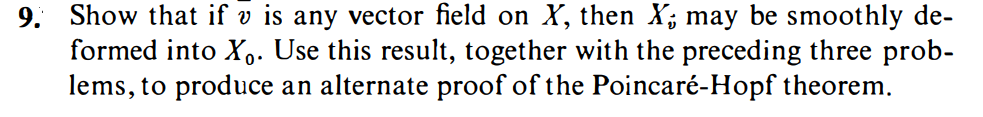
*.--' Recall that a vector eld 33 on a manifold X in R\" is a particular type of _ map : X > R\". Show that at a zero 3:, the derivative dieix : TAX) > R\" actually carries TAX) into itself. [HIN'rz le = R\" x {0}, then the claim is obvious. But you can always reduce to this case by Suitable local parametrizations around I in R\".] \f\f7-1 Zeros of vector elds may be \"split" by perturbations just like xed points of maps. Suppose that x is a zero of; and U is a neighborhood of x in X containing no other zero.of' ii. Prove that there exists a vector eld 31 that agrees with 3 outside some compact subset of U and that has only nondegenerate xed points inside U. [HINT: Reduce to the caSe where U is an open subset of R". Pick a function p that is 1 near x and 0 outside a compact subset of U, and dene 31(2) = \"5(2) 4- p003, E e R\". Show that if; is small enough, 51 can be zero only where p E 1. Now demand that a be a regular value of 1).] \f\f