please provide with full working solution.

thanks so much for your help.

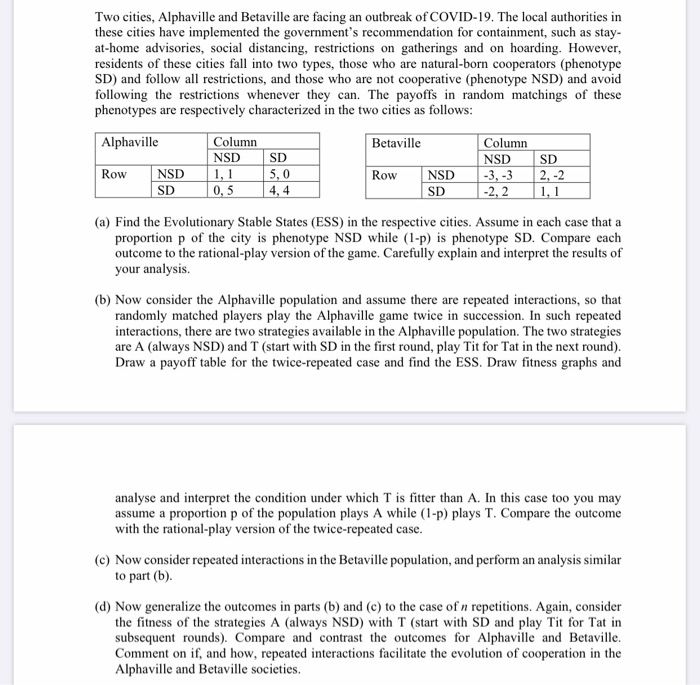
Two cities, Alphaville and Betaville are facing an outbreak of COVID-19. The local authorities in these cities have implemented the government's recommendation for containment, such as stay- at-home advisories, social distancing, restrictions on gatherings and on hoarding. However, residents of these cities fall into two types, those who are natural-born cooperators (phenotype SD) and follow all restrictions, and those who are not cooperative (phenotype NSD) and avoid following the restrictions whenever they can. The payoffs in random matchings of these phenotypes are respectively characterized in the two cities as follows: Alphaville Betaville Column NSD 1,1 0,5 Row NSD SD 5,0 4,4 Row NSD Column NSD SD -3, -3 | 2-2 -2,2 1,1 SD SD (a) Find the Evolutionary Stable States (ESS) in the respective cities. Assume in each case that a proportion p of the city is phenotype NSD while (1-P) is phenotype SD. Compare each outcome to the rational-play version of the game. Carefully explain and interpret the results of your analysis. (b) Now consider the Alphaville population and assume there are repeated interactions, so that randomly matched players play the Alphaville game twice in succession. In such repeated interactions, there are two strategies available in the Alphaville population. The two strategies are A (always NSD) and T (start with SD in the first round, play Tit for Tat in the next round). Draw a payoff table for the twice-repeated case and find the ESS. Draw fitness graphs and analyse and interpret the condition under which T is fitter than A. In this case too you may assume a proportion p of the population plays A while (1-p) plays T. Compare the outcome with the rational-play version of the twice-repeated case. (C) Now consider repeated interactions in the Betaville population, and perform an analysis similar to part (b). (d) Now generalize the outcomes in parts (b) and (c) to the case of n repetitions. Again, consider the fitness of the strategies A (always NSD) with T (start with SD and play Tit for Tat in subsequent rounds). Compare and contrast the outcomes for Alphaville and Betaville. Comment on if, and how, repeated interactions facilitate the evolution of cooperation in the Alphaville and Betaville societies. Two cities, Alphaville and Betaville are facing an outbreak of COVID-19. The local authorities in these cities have implemented the government's recommendation for containment, such as stay- at-home advisories, social distancing, restrictions on gatherings and on hoarding. However, residents of these cities fall into two types, those who are natural-born cooperators (phenotype SD) and follow all restrictions, and those who are not cooperative (phenotype NSD) and avoid following the restrictions whenever they can. The payoffs in random matchings of these phenotypes are respectively characterized in the two cities as follows: Alphaville Betaville Column NSD 1,1 0,5 Row NSD SD 5,0 4,4 Row NSD Column NSD SD -3, -3 | 2-2 -2,2 1,1 SD SD (a) Find the Evolutionary Stable States (ESS) in the respective cities. Assume in each case that a proportion p of the city is phenotype NSD while (1-P) is phenotype SD. Compare each outcome to the rational-play version of the game. Carefully explain and interpret the results of your analysis. (b) Now consider the Alphaville population and assume there are repeated interactions, so that randomly matched players play the Alphaville game twice in succession. In such repeated interactions, there are two strategies available in the Alphaville population. The two strategies are A (always NSD) and T (start with SD in the first round, play Tit for Tat in the next round). Draw a payoff table for the twice-repeated case and find the ESS. Draw fitness graphs and analyse and interpret the condition under which T is fitter than A. In this case too you may assume a proportion p of the population plays A while (1-p) plays T. Compare the outcome with the rational-play version of the twice-repeated case. (C) Now consider repeated interactions in the Betaville population, and perform an analysis similar to part (b). (d) Now generalize the outcomes in parts (b) and (c) to the case of n repetitions. Again, consider the fitness of the strategies A (always NSD) with T (start with SD and play Tit for Tat in subsequent rounds). Compare and contrast the outcomes for Alphaville and Betaville. Comment on if, and how, repeated interactions facilitate the evolution of cooperation in the Alphaville and Betaville societies