please put the excel formulas so i can understand the process

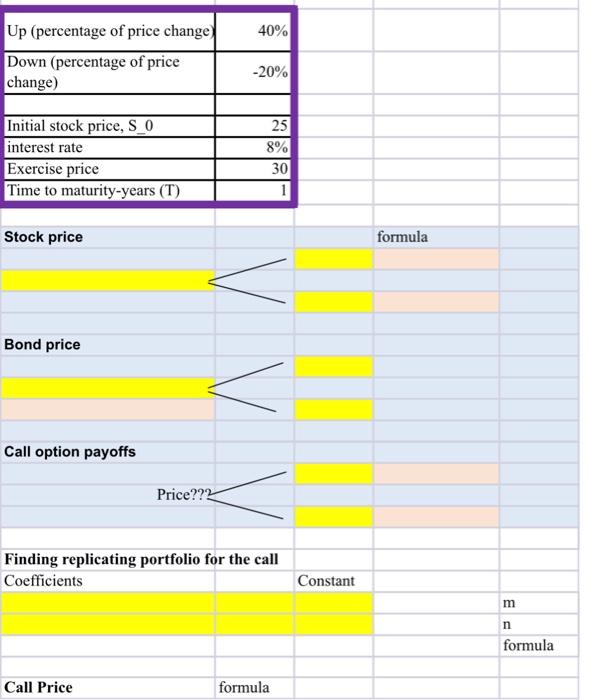
Q1. A stock selling for $25 today will, in 1 year, be worth either $35 (up by 40% ) or $20 (down by 20% ). If the interest rate is 8%. This stock does not pay dividend. There is a 1-year European call option on the stock with exercise price $30. What is the value today of the call option? Please use one-period binomial tree model and assume discrete discounting. (4 points) Q2. Suppose there is also a 1-year European put option on the same stock as in Question 2 with exercise price $30. The current stock price is also $25 and the stock price, in 1 year, will be either $35 (up by 40% ) or $20 (down by 20% ). The interest rate is 8%. This stock does not pay dividend. What is the value of the put option? Please use one-period binomial tree model and assume discrete discounting. (4 points) \begin{tabular}{|l|r|} \hline Up (percentage of price change) & 40% \\ \hline Down(percentageofpricechange) & 20% \\ \hline & 25 \\ \hline Initial stock price, S_0 & 8% \\ \hline interest rate & 30 \\ \hline Exercise price & 1 \\ \hline Time to maturity-years (T) & (T) \end{tabular} Stock price formula Bond price Call option payoffs Price?? Finding replicating portfolio for the call Coefficients Constant Call Price formula Q1. A stock selling for $25 today will, in 1 year, be worth either $35 (up by 40% ) or $20 (down by 20% ). If the interest rate is 8%. This stock does not pay dividend. There is a 1-year European call option on the stock with exercise price $30. What is the value today of the call option? Please use one-period binomial tree model and assume discrete discounting. (4 points) Q2. Suppose there is also a 1-year European put option on the same stock as in Question 2 with exercise price $30. The current stock price is also $25 and the stock price, in 1 year, will be either $35 (up by 40% ) or $20 (down by 20% ). The interest rate is 8%. This stock does not pay dividend. What is the value of the put option? Please use one-period binomial tree model and assume discrete discounting. (4 points) \begin{tabular}{|l|r|} \hline Up (percentage of price change) & 40% \\ \hline Down(percentageofpricechange) & 20% \\ \hline & 25 \\ \hline Initial stock price, S_0 & 8% \\ \hline interest rate & 30 \\ \hline Exercise price & 1 \\ \hline Time to maturity-years (T) & (T) \end{tabular} Stock price formula Bond price Call option payoffs Price?? Finding replicating portfolio for the call Coefficients Constant Call Price formula