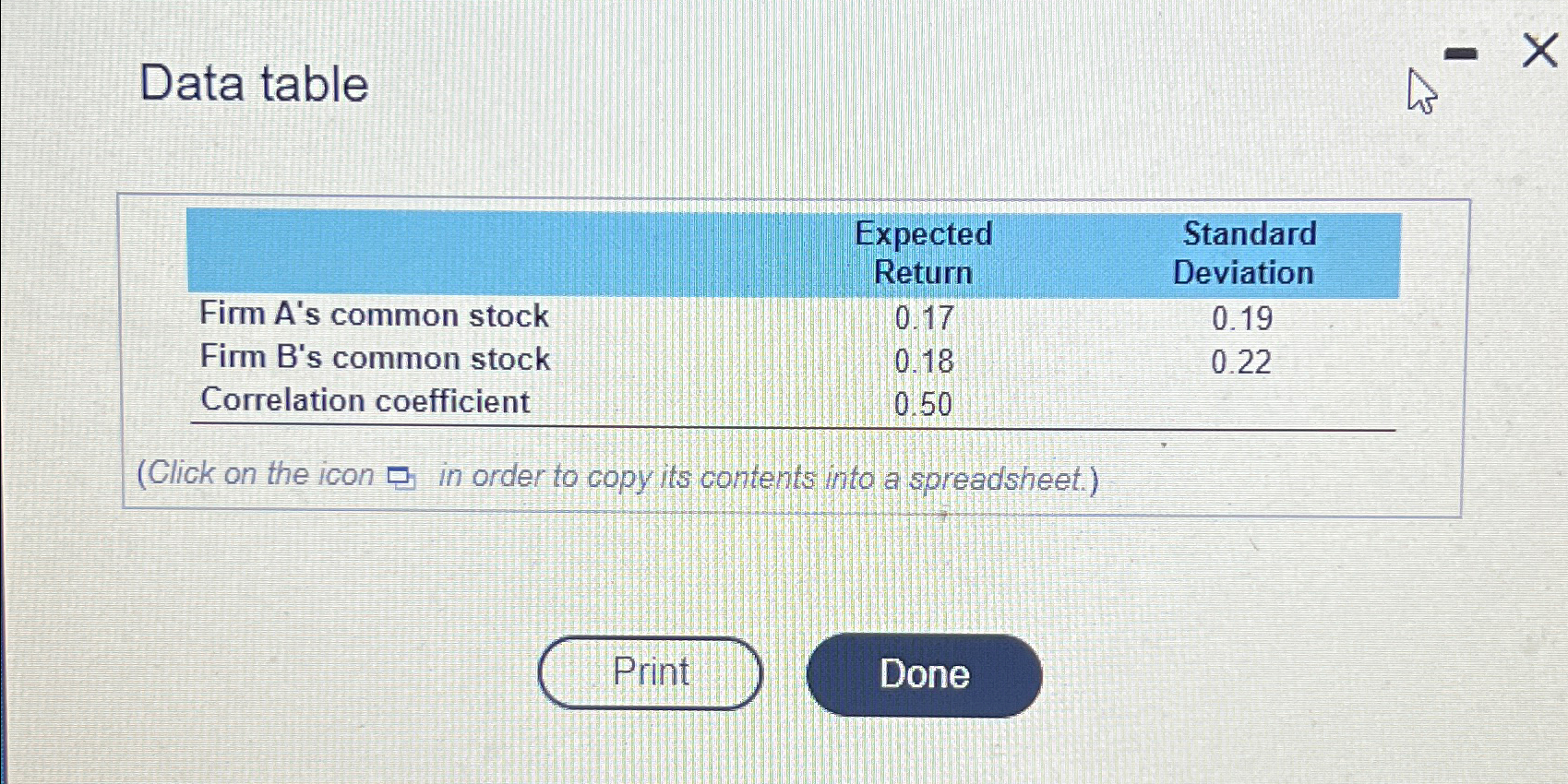
PLEASE READ!$($Computing the standard deviation for a portfolio of two risky investments$)$ Mary Guilott recently graduated from Nichols State University and is anxious to begin investing her meager savings as a way of applying what she has learned in business school. Specifically, she is evaluating an investment in a portfolio comprised of two firms' common stock. She has collected the following information about the common stock of Firm A and Firm B:

a$.$ If Mary invests half her money in each of the two common stocks, what is the portfolio's expected rate of return and standard deviation in portfolio return?

b$.$ Answer part a where the correlation between the two common stock investments is equal to zero.

c$.$ Answer part a where the correlation between the two common stock investments is equal to $+1.$

d$.$ Answer part a where the correlation between the two common stock investments is equal to $-1.$

e$.$ Using your responses to questions a$-$d$,$ describe the relationship between the correlation and the risk and return of the portfolio.

a$.$ If Mary decides to invest $50\%$ of her money in Firm A$\text{'}$s common stock and $50\%$ in Firm B$\text{'}$s common stock and the correlation between the two stocks is $0\mathrm{.}50,$ then the expected rate of return in the portfolio is $\%.($Round to two decimal places.$)$

The standard deviation in the portfolio is $\%.($Round to two decimal places.$)$

b$.$ If Mary decides to invest $50\%$ of her money in Firm A$\text{'}$s common stock and $50\%$ in Firm B$\text{'}$s common stock and the correlation between the two stocks is zero, then the expected rate of return in the portfolio is $\%.($Round to two decimal places$)$

The standard deviation in the portfolio is $\%.($Round to two decimal places$)$

c$.$ If Mary decides to invest $50\%$ of her money in Firm A$\text{'}$s common stock and $50\%$ in Firm B$\text{'}$s common stock and the correlation coefficient between the two stocks is $+1,$

$($Computing the standard deviation for a portfolio of two risky investments$)$ Mary Guilott recently graduated from Nichols State University and is anxious to begin investing her meager savings as a way of applying what she has leamed in business school. Specifically, she is evaluating an investment in a portfolio comprised of two firms' common stock. She has collected the following information about the common stock of Firm A and Firm B:

a$.$ If Mary invests half her money in each of the two common stocks, what is the portfolio's expected rate of return and standard deviation in portfolio return?

b$.$ Answer part a where the correlation between the two common stock investments is equal to zero.

c$.$ Answer part a where the correlation between the two common stock investments is equal to $+1.$

d$.$ Answer part a where the correlation between the two common stock investments is equal to $-1.$

e$.$ Using your responses to questions a$-$d$,$ describe the relationship between the correlation and the risk and return of the portfolio.

a$.$ If Mary decides to invest $50\%$ of her money in Firm A$\text{'}$s common stock and $50\%$ in Firm B$\text{'}$s common stock and the correlation between the two stocks is $0\mathrm{.}50,$ then the expected rate of return in the portfolio is $\_\%.($Round to two decimal places.$)$

The standard deviation in the portfolio is $\_\%.($Round to two decimal places.$)$

b$.$ If Mary decides to invest $50\%$ of her money in Firm A$\text{'}$s common stock and $50\%$ in Firm B$\text{'}$s common stock and the correlation between the two stocks is zero, then the expected rate of return in the portfolio is $\_\%.($Round to two decimal places.$)$

The standard deviation in the portfolio is $\%.($Round to two decimal places.$)$

c$.$ If Mary decides to invest $50\%$ of her money in Firm A$\text{'}$s common stock and $50\%$ in Firm B$\text{'}$s common stock and the correlation coefficient between the two stocks is $+1,$ then the expected rate of return in the portfolio is $\_\%.$

The standard deviationin the portfolio is $\_\%.$

d$.$ If Mari decides to invest $50\%$ of her money and firm A$\text{'}$s common stock, and $50\%$ in firm B$\text{'}$s common stock and the correlation coefficient between the two stocks is $-1,$ then the expected rate of return in the portfolio is $\_\%$

The standard deviation in the portfolio is $\_\%.$

e$.$ Using your responses to question a through D$,$ which of the following statements, best describes the relationship between the correlation, and the risk and return of the portfolio?$($multiple choice$)$

A$.$ The correlation coefficient has no effect on the expected return of a portfolio, but the closer the correlation coefficient is to negative one, the lower the risk.

B$.$The correlation coefficient has a negative effect on the expected return of a portfolio and the closer the correlation coefficient is to negative one, the lower the risk.

C$.$ The correlation coefficient has no effect on the expected return of a portfolio, but the closer the correlation coefficient is to one, the lower the risk.

D$.$ The correlation coefficient has no effect on the expected return of a portfolio, but the closer the correlation coefficient is to $-1$ the higher, the risk.