Please reference the Black and Scholes data attachments.

Current stock price is S0= 80, the annual stock volatility is ? = 40%, and the annual

dividend yield is ? = 0. The current risk-free interest rate is r = .01 = 1%.

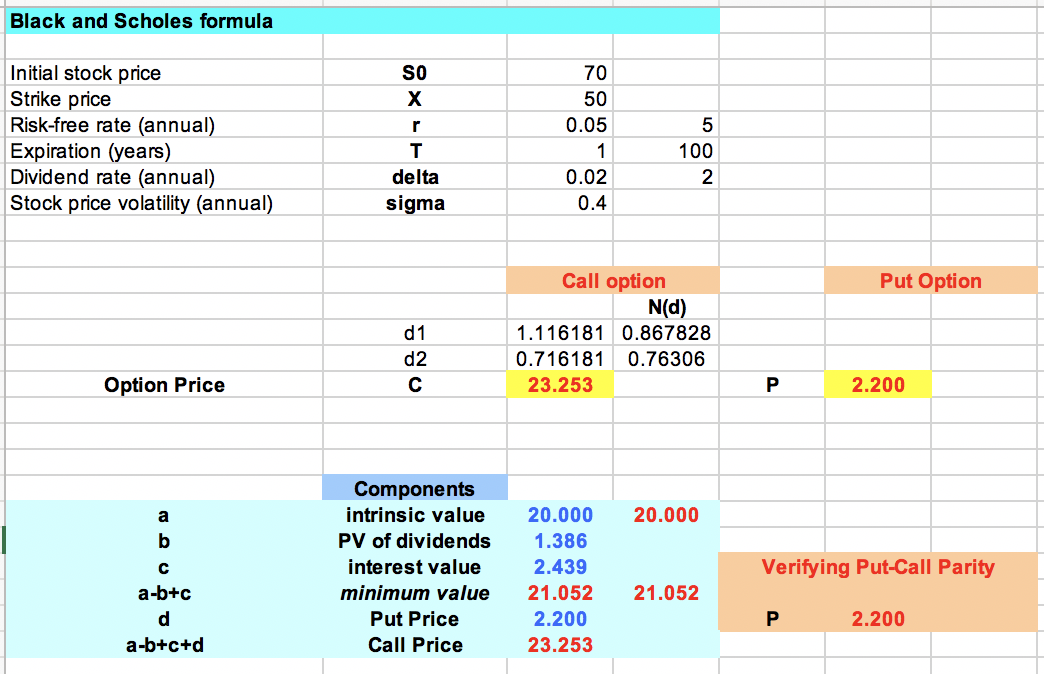
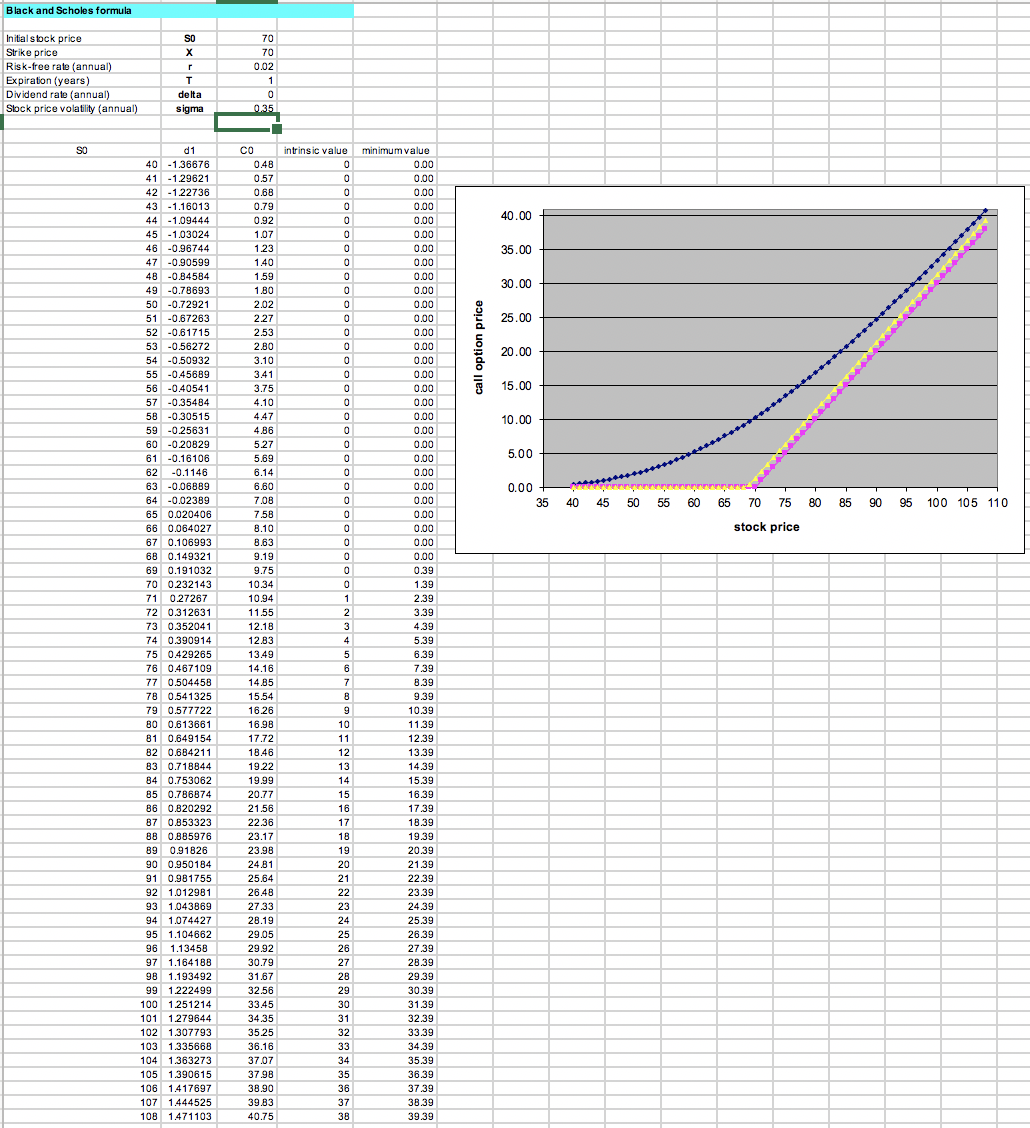
(a)Calculate the Black-Scholes prices of call options with strike K = 80 and maturity of 1, 5, 10, 50, and 100 years. What will happen to call option prices as the time to maturity keeps increasing?

(b)Keeping every other parameter constant, suppose the dividend yield is now ? = 0.01 = 1%. Again, calculate call option prices for strike K = 80 at the above maturities. What happens to option prices as time to maturity increases?

(c)What explains the difference between (a) and (b)?

Black and Scholes formula Initial stock price SO 70 Strike price X 50 Risk-free rate (annual) r 0.05 5 Expiration (years) T 1 100 Dividend rate (annual) delta 0.02 2 Stock price volatility (annual) sigma 0.4 Call option Put Option N(d) d1 1.116181 0.867828 d2 0.716181 0.76306 Option Price C 23.253 P 2.200 Components a intrinsic value 20.000 20.000 b PV of dividends 1.386 C interest value 2.439 Verifying Put-Call Parity a-b+c minimum value 21.052 21.052 d Put Price 2.200 P 2.200 a-b+c+d Call Price 23.253Black and Scholes formula Initial stock price Strike price 70 - X g 70 Risk-free rate (annual) 0.02 Expiration (years) 1 Dividend rate (annual) delta Stock price volatility (annual) sigma 0.35 SO d1 CO intrinsic value |minimum value 40 -1.36676 0.48 0 41 -1.29621 0.00 0.57 0.00 12 -1.22736 0.68 43 -1.16013 0.00 0.79 0.00 14 -1.0944 0.92 0.00 40.00 45 -1.03024 1.07 46 -0.96744 0.00 1.23 0.00 47 -0.90599 1.40 35.00 0.00 48 -0.84584 1.59 19 -0.78693 o 0.00 1.80 0.00 30.00 50 -0.72921 2.02 0.00 51 -0.67263 2.27 0.00 52 -0.61715 25.00 2.53 53 -0.56272 0.00 2.80 0.00 call option price 54 -0.50932 3.10 20.00 65 -0.45689 0.00 3.41 56 -0.40541 0.00 3.75 57 -0.35484 0.00 15.00 4.10 58 0.00 4.47 0.00 19 -0.25631 4.86 10.00 0.00 60 -0.20829 5.27 0.00 -0.16106 5.69 -0.1146 0.00 5.00 6.14 0.00 -0.06889 6.60 0.00 64 -0.02389 7.08 0.00 - 5 0.02040 0.00 7.58 35 0.00 40 45 50 55 60 65 70 75 80 85 90 86 0.064027 8.10 95 100 105 110 67 0.106993 0.00 8.63 38 0.149321 0.00 stock price 9.19 0.00 39 0.191032 9.75 0.39 0.232143 10.34 1.39 71 0.27267 10.94 72 0.312631 2.39 11.55 3.39 3 0.352041 12.18 74 0.390914 4.39 12.83 5.39 5 0.429265 13.49 6.39 76 0467109 14.16 77 0.504458 7.39 78 0.541325 8.39 15.54 9.39 9 0.577722 8 16.26 10.39 30 0.613661 16.98 11.39 81 0.649154 17.72 12.39 82 0.684211 18.46 12 13.39 83 0.718844 19.22 13 14.39 0.753062 19.99 14 15.39 35 0.786874 20.77 15 86 0.820292 21.56 16 16.39 17.39 37 0.853323 22.36 17 18.39 88 23.17 18 0.91826 19.39 23.98 19 20.39 90 0.950184 24.81 20 21.39 91 25.64 21 22.39 26.48 22 1.043869 23.39 27 33 23 34 1.074427 24.39 28.19 24 25.39 15 1.104662 29.05 25 1.13458 26.39 29.92 26 27.39 97 1.164188 30.79 27 98 1.193492 28.39 31.67 28 99 1.222499 29.39 32.56 29 30.39 00 1.251214 33.45 30 01 1279644 31.39 34.35 31 32.39 102 1.307793 35.25 103 32 33.39 1.335668 6.16 33 34.39 104 1.363273 37.07 34 105 1.390615 35.39 37.98 35 6 1.417697 36.39 38.90 36 37.39 107 1.444525 39.83 37 08 1.471103 40.75 38 38.39 39.39