Please show all work/steps. Please do not use excel or other programs. Thanks

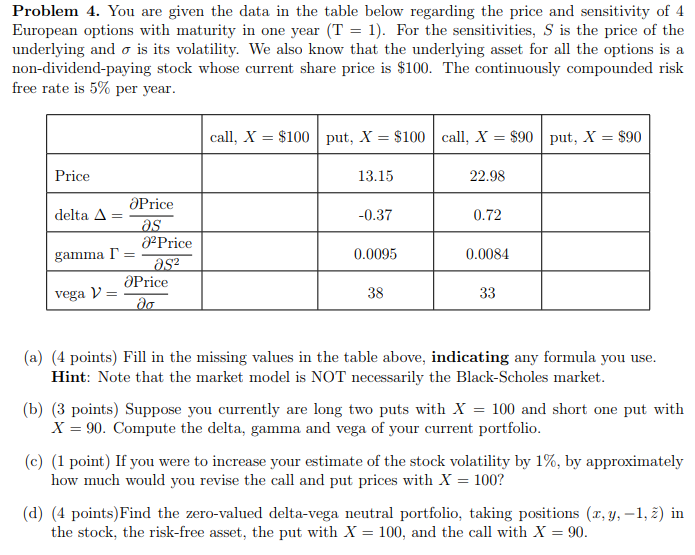
Problem 4. You are given the data in the table below regarding the price and sensitivity of 4 European options with maturity in one year (T-1. For the sensitivities, S is the price of the underlying and is its volatility. We also know that the underlying asset for all the options is a non-dividend-paying stock whose current share price is $100. The continuously compounded risk free rate is 5% per year call, X = $100 | put, X S 100 | call. X = $90 | put, X = $90 13.15 0.37 0.0095 22.98 0.72 0.0084 rice OPrice delta = 2Price gamma OPrice vega V= 38 (a) (4 points) Fill in the missing values in the table above, indicating any formula you use Hint: Note that the market model is NOT necessarily the Black-Scholes market (b) (3 points) Suppose you currently are long two puts with X = 100 and short one put with (c) (1 point) If you were to increase your estimate of the stock volatility by 1%, by approximately d) (4 points)Find the zero-valued delta-vega neutral portfolio, taking positions (x, y,-1, ) in X = 90. Compute the delta, gamma and vega of your current portfolio how much would you revise the call and put prices with X = 100? the stock, the risk-free asset, the put with X = 100, and the call with X = 90 Problem 4. You are given the data in the table below regarding the price and sensitivity of 4 European options with maturity in one year (T-1. For the sensitivities, S is the price of the underlying and is its volatility. We also know that the underlying asset for all the options is a non-dividend-paying stock whose current share price is $100. The continuously compounded risk free rate is 5% per year call, X = $100 | put, X S 100 | call. X = $90 | put, X = $90 13.15 0.37 0.0095 22.98 0.72 0.0084 rice OPrice delta = 2Price gamma OPrice vega V= 38 (a) (4 points) Fill in the missing values in the table above, indicating any formula you use Hint: Note that the market model is NOT necessarily the Black-Scholes market (b) (3 points) Suppose you currently are long two puts with X = 100 and short one put with (c) (1 point) If you were to increase your estimate of the stock volatility by 1%, by approximately d) (4 points)Find the zero-valued delta-vega neutral portfolio, taking positions (x, y,-1, ) in X = 90. Compute the delta, gamma and vega of your current portfolio how much would you revise the call and put prices with X = 100? the stock, the risk-free asset, the put with X = 100, and the call with X = 90