Question: Please show c and d in k and k This problem concerns the Arithmetic Hierarchy, which is at the top of the World-of-Computability-and Complexity diagram.

Please show c and d in 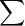 k and
k and 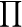 k
k
This problem concerns the Arithmetic Hierarchy, which is at the top of the World-of-Computability-and Complexity diagram. We say that a set of natural numbers, S, is an element of ?, iff there is a PTIME predicate p, such that here Qk is V if k is even and 3 if k is odd. Similarly, S is an element of IT iff for some PTIME predicate v. Here Q. is V if k is odd and ? if k is even. Define the Arithmetic Hierarchy to be UEL ?k. Classify the following sets by writing a formula that places them as low as you can in the arithmetic hierarchy. You do not have to prove that they cannot be placed in a lower class, For example. TOTAL = {n | Mn halts on all inputs} is ?2 because it can be written as TOTAL {n|Va32(COMP(n.r, L(z), R(z)))). = [A PTIME predicate, ?, is just a PTIME computable decider-for each possible input it answers "true" or false" in PTIME. COMP(n, r,c, y) is the PTIME predicate meaning that c is a complete halting com- putation of TM M on input x and its output is y. Recall that we defined Cantor's pairing function: P N x N N. given by P(i.jC)i and it's inverses, L, R where L(P(x,y)) R(P(x, y)) y and P(L(), R(z)) z. The pairing function makes it clear that in the above definition there is no change if we have multiple quantifiers of the same kind, i.e. 3r3y has the same power as 3z. From now on, let's let N 0,.. (d) FINITETM= {n I is finite} This problem concerns the Arithmetic Hierarchy, which is at the top of the World-of-Computability-and Complexity diagram. We say that a set of natural numbers, S, is an element of ?, iff there is a PTIME predicate p, such that here Qk is V if k is even and 3 if k is odd. Similarly, S is an element of IT iff for some PTIME predicate v. Here Q. is V if k is odd and ? if k is even. Define the Arithmetic Hierarchy to be UEL ?k. Classify the following sets by writing a formula that places them as low as you can in the arithmetic hierarchy. You do not have to prove that they cannot be placed in a lower class, For example. TOTAL = {n | Mn halts on all inputs} is ?2 because it can be written as TOTAL {n|Va32(COMP(n.r, L(z), R(z)))). = [A PTIME predicate, ?, is just a PTIME computable decider-for each possible input it answers "true" or false" in PTIME. COMP(n, r,c, y) is the PTIME predicate meaning that c is a complete halting com- putation of TM M on input x and its output is y. Recall that we defined Cantor's pairing function: P N x N N. given by P(i.jC)i and it's inverses, L, R where L(P(x,y)) R(P(x, y)) y and P(L(), R(z)) z. The pairing function makes it clear that in the above definition there is no change if we have multiple quantifiers of the same kind, i.e. 3r3y has the same power as 3z. From now on, let's let N 0,.. (d) FINITETM= {n I is finite}
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


