Question: Please Show the work thank you ! 3. Consider the data points (xo, fo), (21, f1), ..., (In, fn), where the points To, X1, .
Please Show the work thank you !

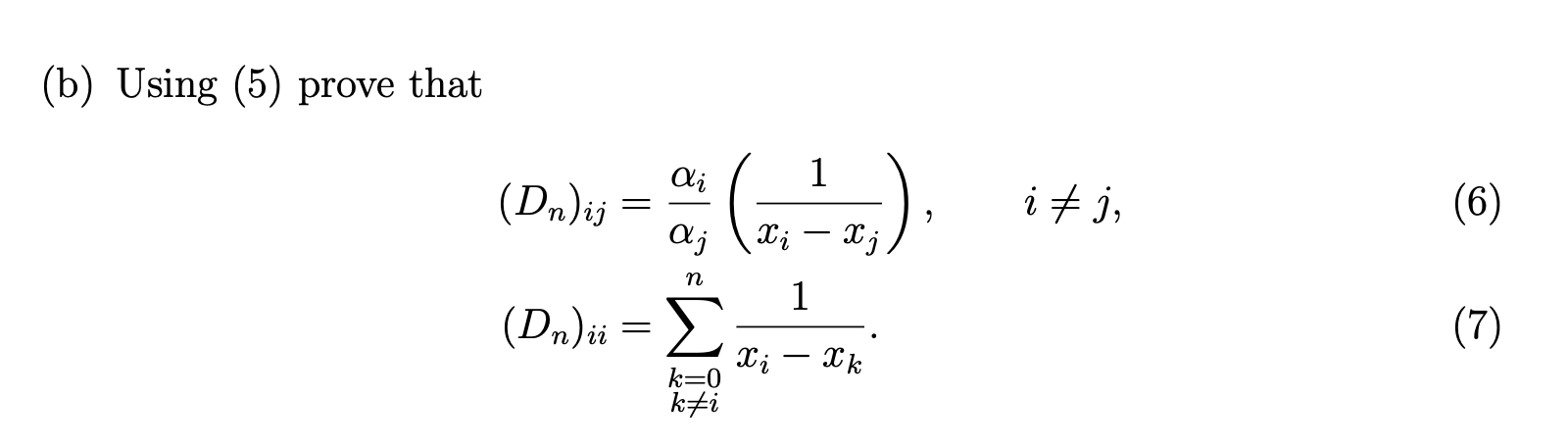
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


