Please show work with WRITTEN instructions, i'm so confused. Conclude if Snell Law is satisfied.

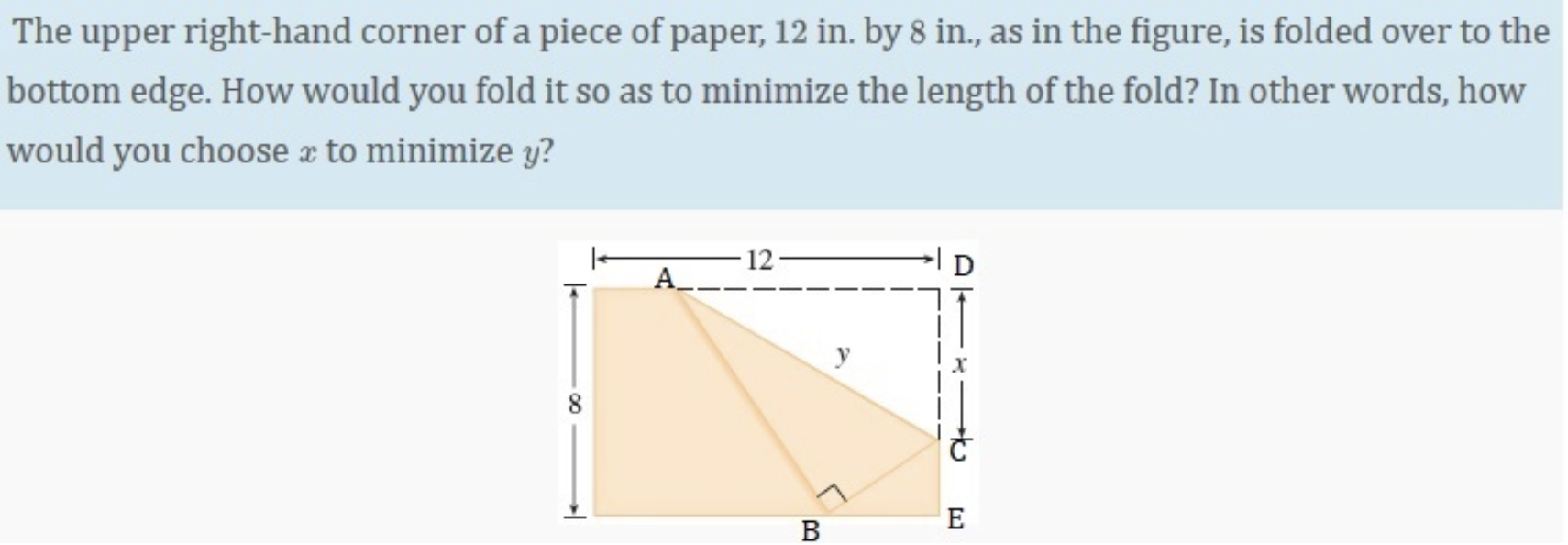
The upper right-hand corner of a piece of paper, 12 in. by 8 in., as in the figure, is folded over to the bottom edge. How would you fold it so as to minimize the length of the fold? In other words, how would you choose a to minimize y? A 12 D X 8 B E(a) Copy the diagram and put the labels , 'D' and 'E' at the right angle corners of the two right triangles so that AADC' is the right triangle above the water and ABEC is the right triangle under the water. We will add our own assumptions as follows: IADI = |BE| = 1 and |DE| = 2. (Then: is a may to show that making such arbitrary assumptions do not alter the nature of this problem. At this moment, don't mom'y about it.) (b) Let t denote the tinle spent by the photon to go from A to B via C. [Assume AC and CB are both straight lines] Also, let x = IDCI and y = ICE|. Express t as a function of a: and 1;. Your expression will contain two constants, 1:1 and v2 (speeds of light in two dierent media.) They are not variables! (c) Write the relationship between a: and 3;. Using this constraint, rewrite t as a function of so alone and pick a reasonable domain. It's better to have a compact domain (in interval of the form [(1, b]. (d) Find the derivative % and show that (it _ m _ '9' da: \"on/m 1:2ng (e) Show (by using Intermediate Theorem)I that g has at least one zero on the interval that you chose in (c). Check to see if all the conditions for IVT are satised. (f) Show that there is no other zero for %. [ Hint: Show that g > 0 on the entire open interval contained in your domain. Then, use a standard argument using the Mean Value Theorem. ] (g) Show that t achieves its absolute minimum at the (unique) critical number that we discussed in (f) (g) above. [HintI Use the fact that 3: > U for all a: and the MVT to show that ('11; > U for all a; to the right of this critical number and f;