Please solve 4-7.

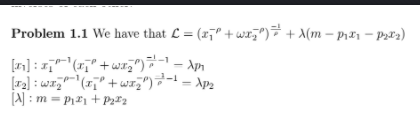
\f1 CES utility function Suppose that the consumer has utility function u(x1, 12) = (TP + WI,) . The consumer faces the budget constraint pit, + p2$2 = m. 1. Let ro denote the Marshallian demand of good i. Show that ry = KIM i.e. the Marshallian demand of good 2 is proportional to the Marshallian demand of good 1 (or some given reference good). What is k? 2. Derive my as a function of (p1, p2, m). 3. What is the value of A*? Show that A" is proportional to the indirect utility function v(p1, p2, m). 4. Derive the elasticity of substitution between two goods. Is it interesting? 5. Derive the Hicksian demand functions, along with an expenditure func- tion. 6. Show that the Hicksian demand of (p1, pa, ") is homogeneous of degree 0 in (p1, p2). Also show that the expenditure function e(p1, p2, a) is homogeneous of degree 1 in (p1, p2). (Observe that the homogeneity holds only in terms of prices and not a, unlike the homogeneity property of Marshallian demand as in part 1.9. ) 7. Calculate n' explicitly from the cost minimization problem. How is this related to A*