Please solve

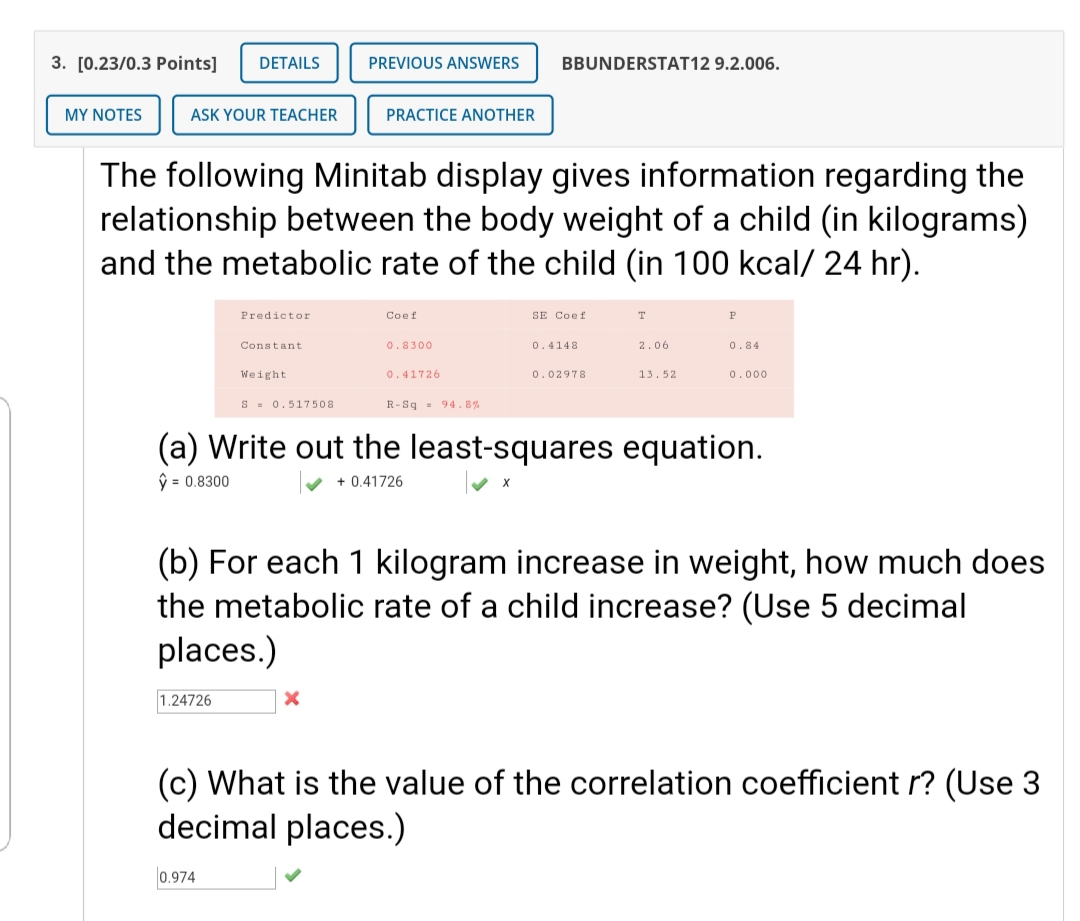
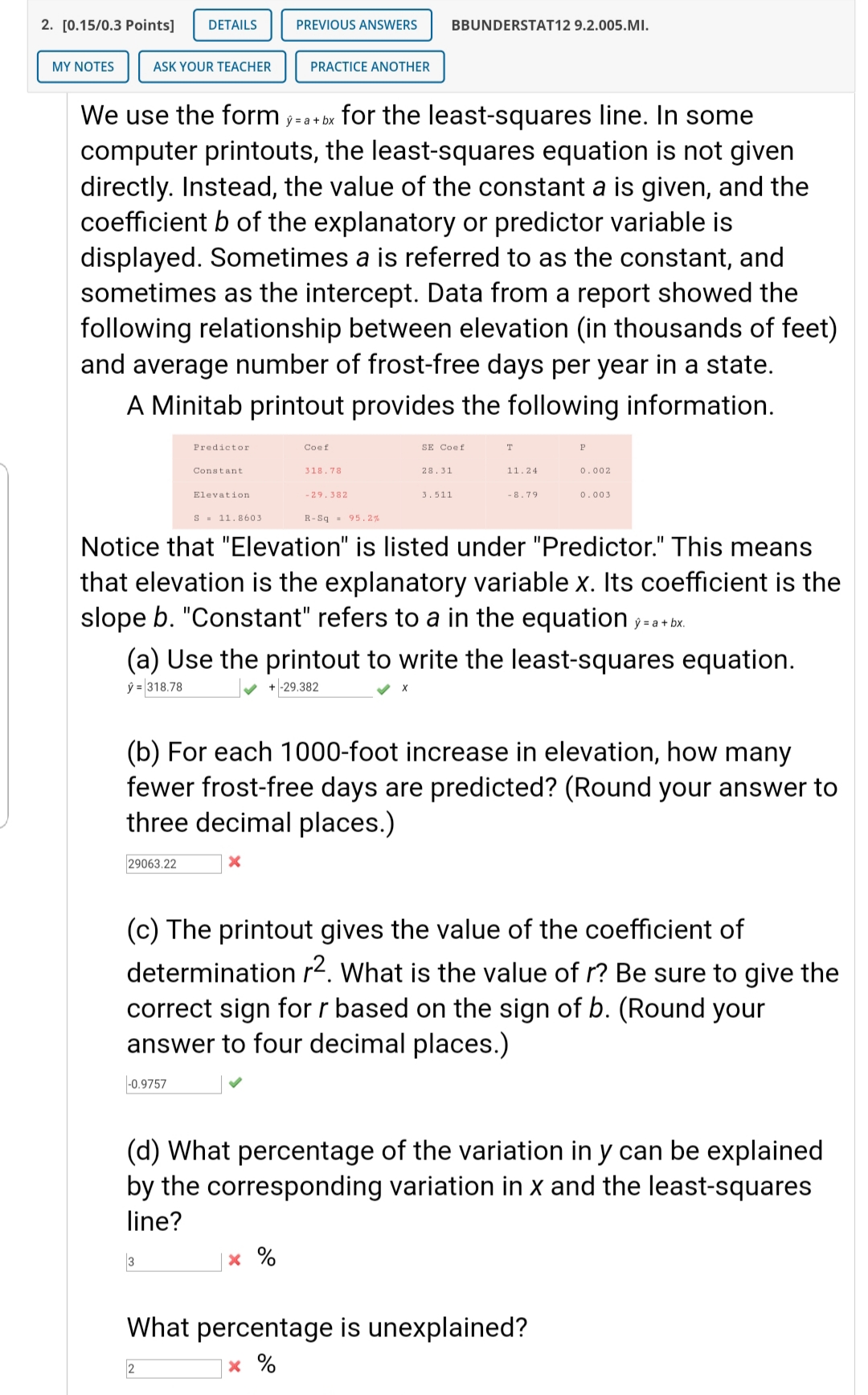
9. [0.181113 Points] BBUNDERSTAT129.2.021.NVA \\ MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER / (a) Suppose you are given the following (x, y) data pairs. I'll um Find the least-squares equation for these data (rounded to three digits after the decimal). A y = 1.353r X + 1.?14 8 X (b) Now suppose you are given these (x, y) data pairs. [.439 "134 Find the least-squares equation for these data (rounded to three digits after the decimal). )7 = |0.3065 |x + 1.032 |x X (c) In the data for parts (a) and (b), did we simply exchange the x and y values of each data pair? ' Yes No J (d) Solve your answer from part (a) for x (rounded to three digits after the decimal). - 4.253 | + 0.73? |~I y Do you get the least-squares equation of part (b) with the symbols X and y exchanged? Yes 'No J 3. [0.23I0.3 Points] DETAILS PREVIOUS ANSWERS BBUNDERSTAT12 9.2.006. MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER The following Minitab display gives information regarding the relationship between the body weight of a child (in kilograms) and the metabolic rate of the child (in 100 kcal/ 24 hr). Predictor CDEf SE Gael T P Constant 0.8300 0.4143 2.06 0.34 Weight 0.91726 0.02978 15.52 0.000 S x 0.511508 RSq x 99.8% (a) Write out the least-squares equation. 9: 0.0300 | + 0.41720 | x (b) For each 1 kilogram increase in weight, how much does the metabolic rate of a child increase? (Use 5 decimal places.) [1.24726 | x (c) What is the value of the correlation coefcient r? (Use 3 decimal places.) |0.974 | J 2. [0.15103 Points] BBUNDERSTAT129.2.005.MI. We use the form PM. for the least-squares line. In some computer printouts, the least-squares equation is not given directly. Instead, the value of the constant a is given, and the coefcient b of the explanatory or predictor variable is displayed. Sometimes a is referred to as the constant, and sometimes as the intercept. Data from a report showed the following relationship between elevation (in thousands of feet) and average number of frost-free days per year in a state. A Minitab printout provides the following information. Predictor Cuef SE Cost '1' P Constant 315.78 28.31 11.24 0.002 Elev-{inn -2?.382 3.511 -B.19 0.00} S = 11.8603 R-Sq = 95.2% Notice that "Elevation" is listed under "Predictor." This means that elevation is the explanatory variable x. Its coefficient is the slope b. "Constant" refers to a in the equation mm. (a) Use the printout to write the least-squares equation. y=|3ia.?s | +|-29.332 x (b) For each 1000-foot increase in elevation, how many fewer frost-free days are predicted? (Round your answer to three decimal places.) |2906322 l x (c) The printout gives the value of the coefficient of determination r2. What is the value of r\"? Be sure to give the correct sign for r based on the sign of b. (Round your answer to four decimal places.) |-o.9757 l v (d) What percentage of the variation in y can be explained by the corresponding variation in x and the least-squares line? |3 lx 0/0 What percentage is unexplained? |2 ix 0/0