PLEASE SOLVE BY USING MATLAB. I've upload all three question because they are connected.

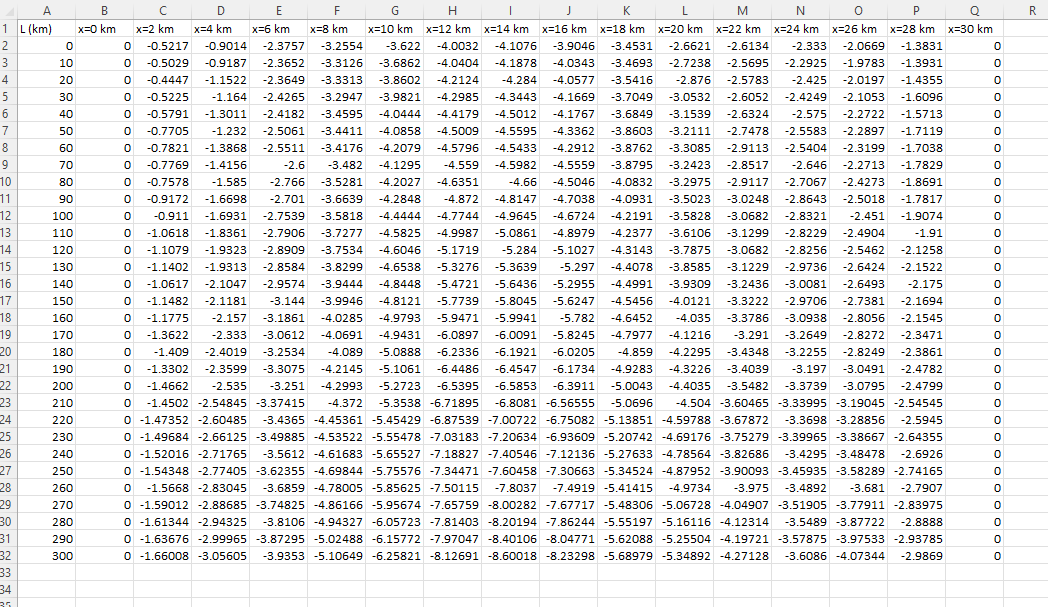
QUESTION 1 (15 marks) Setting up cables for undersea power transmission is far from simple and much more complex than overhead transmission on land. Measuring and mapping the desired ocean section bed is of paramount importance for planning, installation and commissioning the cables properly to ensure minimal maintenance and durability. The picture shows a typical installation phase of submarine cable installation. In certain sections, discrete depth measurement is required to ensure an accurate measurement and mapping of the ocean bed. Assume you are project engineer in an undersea power cable installation project, and you need to employ numerical methods to verify the mapping a certain part of cross-sectional areas. A schematic of the ocean bed cross-section is presented in figure 1. Survey results for a certain small cross-section, which is spread over 30 km width and 305 km long. The survey team recorded the depths up to 9 km in several areas along the 305 km length section. The data details can be found in the "Ocean_bed_data.xlsx file. In this file, L and x represent the length and width of the desired section of the ocean bed. Note that negative values in the excel file indicate depths as the depth is measured from the water surface to downwards to reach the desired location of the ocean bed. Q1(a) (3 marks) Import the data from the "Ocean_bed_data.xlsx" file. Make sure that all units are consistent. For six equally spaced locations along the 300 km long section, plot the corresponding depth vs width data in a 3-by-2 subplot configuration in figure (1). Plot the data using red circles and use the location (i.e., length, L = 0 m) information in the title for each subplot. Hint: Use a for loop to plot and use sprintf() to print the titles for each subplot. Q1(b) (4 marks) Use the composite trapezoidal rule to integrate the depth data of each cross section from L = 0 to 300 km to calculate the cross-sectional areas, X-area. Consider using only the positive values for X- area. Print the obtained X-area and corresponding location (3 decimal places) in a text file named "X- area.txt". The print format inside the file should look like following table Location (km) X-area (km2) 0 10 xxx.xxx 20 30 40 xxx.xxx xxx.xxx xxx.xxx xxx.xxx Hints: Use a function file to compute the composite trapezoidal rule for vectors. You might consider using the abs() function to take the absolute X-area values. Q1(c) (8 marks) (1) Plot the X-area against the location (length) data obtained in 01(b) with black diamonds in figure (2). Calculate the volume of the ocean bed stretching the length (L=0 to 300 km) using Simpson's 1/3rd rule. Print the result using fprintf(). Can you also calculate the volume using Simpson's 3/8th rule for this data set? Print your thoughts using another fprintf(). (i) During the installation phase, the project team noticed a rise in the ocean bed in the negative L direction due to the reduction of the cross-sectional area, X-area, which can be described by the following equation, 7 Xarea 10BL where L is the location. Fit the X-area and location data for the above-mentioned relationship. Plot this relationship using a suitable range of L value (i.e. from-305 km SLS 305 km) as a blue dashed line in the same figure (figure 2). (ii) Use any suitable root finding methods to determine the location for X-area = 50 km2. Use a red diamond to mark this location on the same figure. Print the root as an answer. Include legend for the figure in a suitable place so it does not overlap any part of the plots. Hints: you can use polyfit() function to fit the data and extract a and values. R 20 A B 1 L(km) x=0 km 2 0 3 10 4 5 5 30 6 6 40 7 2 50 8 60 9 70 10 80 11 90 12 100 13 110 14 120 15 130 16 140 17 150 18 160 19 170 20 180 20 21 190 22 200 23 210 24 220 25 230 26 240 27 250 28 260 29 270 30 280 31 290 32 300 33 34 30 D E F G H M N 0 P Q x=2 km x=4 km x=6 km x=8 km x=10 km x=12 km x=14 km x=16 km x=18 km x=20 km x=22 km x=24 km xx=26 km x=28 km x=30 km 0 -0.5217 -0.9014 -2.3757 -3.2554 -3.622 -4.0032 -4.1076 -3.9046 -3.4531 -2.6621 -2.6134 -2.333 -2.0669 -1.3831 0 0 -0.5029 -0.9187 -2.3652 -3.3126 -3.6862 -4.0404 -4.1878 -4.0343 -3.4693 -2.7238 -2.5695 -2.2925 -1.9783 -1.3931 0 0 -0.4447 -1.1522 -2.3649 -3.3313 -3.8602 -4.2124 -4.284 -4.0577 -3.5416 -2.876 -2.5783 -2.425 -2.0197 -1.4355 0 0 -0.5225 -1.164 -2.4265 -3.2947 -3.9821 -4.2985 -4.3443 -4.1669 -3.7049 -3.0532 -2.6052 -2.4249 -2.1053 -1.6096 0 0 0 -0.5791 -1.3011 -2.4182 -3.4595 -4.0444 -4.4179 -4.5012 -4.1767 -3.6849 -3.1539 -2.6324 -2.575 -2.2722 -1.5713 0 o 0 -0.7705 -1.232 -2.5061 -3.4411 -4.0858 -4.5009 -4.5595 -4.3362 -3.8603 -3.2111 -2.7478 -2.5583 -2.2897 -1.7119 0 0 -0.7821 -1.3868 -2.5511 -3.4176 -4.2079 -4.5796 -4.5433 -4.2912 -3.8762 -3.3085 -2.9113 -2.5404 -2.3199 -1.7038 0 0 -0.7769 -1.4156 -2.6 -3.482 -4.1295 -4.559 -4.5982 -4.5559 -3.8795 -3.2423 -2.8517 -2.646 -2.2713 -1.7829 0 0 -0.7578 -1.585 -2.766 -3.5281 -4.2027 -4.6351 -4.66 -4.5046 -4.0832 -3.2975 -2.9117 -2.7067 -2.4273 -1.8691 0 0 -0.9172 -1.6698 -2.701 -3.6639 -4.2848 -4.872 -4.8147 -4.7038 -4.0931 -3.5023 -3.0248 -2.8643 -2.5018 -1.7817 0 0 -0.911 -1.6931 -2.7539 -3.5818 -4.4444 -4.7744 -4.9645 -4.6724 -4.2191 -3.5828 -3.0682 -2.8321 -2.451 -1.9074 0 0 -1.0618 -1.8361 -2.7906 -3.7277 -4.5825 -4.9987 -5.0861 -4.8979 -4.2377 -3.6106 -3.1299 -2.8229 -2.4904 -1.91 0 0 0 -1.1079 -1.9323 -2.8909 -3.7534 -4.6046 -5.1719 -5.284 -5.1027 -4.3143 -3.7875 -3.0682 -2.8256 -2.5462 -2.1258 0 0 -1.1402 -1.9313 -2.8584 -3.8299 -4.6538 -5.3276 -5.3639 -5.297 -4.4078 -3.8585 -3.1229 -2.9736 -2.6424 -2.1522 0 0 -1.0617 -2.1047 -2.9574 -3.9444 -4.8448 -5.4721 -5.6436 -5.2955 -4.4991 -3.9309 -3.2436 -3.0081 -2.6493 -2.175 0 0 -1.1482 -2.1181 -3.144 -3.9946 -4.8121 -5.7739 -5.8045 -5.6247 -4.5456 -4.0121 -3.3222 -2.9706 -2.7381 -2.1694 0 0 -1.1775 -2.157 -3.1861 -4.0285 -4.9793 -5.9471 -5.9941 -5.782 -4.6452 -4.035 -3.3786 -3.0938 -2.8056 -2.1545 0 0 -1.3622 -2.333 -3.0612 -4.0691 -4.9431 -6.0897 -6.0091 -5.8245 -4.7977 -4.1216 -3.291 -3.2649 -2.8272 -2.3471 0 0 0 -1.409 -2.4019 -3.2534 -4.089 -5.0888 -6.2336 -6.1921 -6.0205 -4.859 -4.2295 -3.4348 -3.2255 -2.8249 -2.3861 0 0 -1.3302 -2.3599 -3.3075 -4.2145 -5.1061 -6.4486 -6.4547 -6.1734 -4.9283 -4.3226 -3.4039 -3.197 -3.0491 -2.4782 0 0 0 -1.4662 -2.535 -3.251 -4.2993 -5.2723 -6.5395 -6.5853 -6.3911 -5.0043 -4.4035 -3.5482 -3.3739 -3.0795 -2.4799 0 o 0 -1.4502 -2.54845 -3.37415 -4.372 -5.3538 -6.71895 -6.8081 -6.56555 -5.0696 -4.504 -3.60465 -3.33995 -3.19045 -2.54545 0 0 -1.47352 -2.60485 -3.4365 -4.45361 -5.45429 -6.87539 -7.00722 -6.75082 -5.13851 -4.59788 -3.67872 -3.3698 -3.28856 -2.5945 0 0 -1.49684 -2.66125 -3.49885 -4.53522 -5.55478 -7.03183 -7.20634 -6.93609 -5.20742 -4.69176 -3.75279 -3.39965 -3.38667 -2.64355 0 0 -1.52016 -2.71765 -3.5612 -4.61683 -5.65527 -7.18827 -7.40546 -7.12136 -5.27633 -4.78564 -3.82686 -3.4295 -3.48478 -2.6926 0 0 -1.54348 -2.77405 -3.62355 -4.69844 -5.75576 -7.34471 -7.60458 -7.30663 -5.34524 -4.87952 -3.90093 -3.45935 -3.58289 -2.74165 0 0 -1.5668 -2.83045 -3.6859 -4.78005 -5.85625 -7.50115 -7.8037 -7.4919 -5.41415 -4.9734 -3.975 -3.4892 -3.681 -2.7907 0 0 -1.59012 -2.88685 -3.74825 -4.86166 -5.95674 -7.65759 -8.00282 -7.67717 -5.48306 -5.06728 -4.04907 -3.51905 -3.77911 -2.83975 0 0 0 -1.61344 -2.94325 -3.8106 -4.94327 -6.05723 -7.81403 -8.20194 -7.86244 -5.55197 -5.16116 -4.12314 -3.5489 -3.87722 -2.8888 0 0 -1.63676 -2.99965 -3.87295 -5.02488 -6.15772 -7.97047 -8.40106 -8.04771 -5.62088 -5.25504 -4.19721 -3.57875 -3.97533 -2.93785 0 0 0 -1.66008 -3.05605 -3.9353 -5.10649 -6.25821 -8.12691 -8.60018 -8.23298 -5.68979 -5.34892 -4.27128 -3.6086 -4.07344 -2.9869 0 QUESTION 1 (15 marks) Setting up cables for undersea power transmission is far from simple and much more complex than overhead transmission on land. Measuring and mapping the desired ocean section bed is of paramount importance for planning, installation and commissioning the cables properly to ensure minimal maintenance and durability. The picture shows a typical installation phase of submarine cable installation. In certain sections, discrete depth measurement is required to ensure an accurate measurement and mapping of the ocean bed. Assume you are project engineer in an undersea power cable installation project, and you need to employ numerical methods to verify the mapping a certain part of cross-sectional areas. A schematic of the ocean bed cross-section is presented in figure 1. Survey results for a certain small cross-section, which is spread over 30 km width and 305 km long. The survey team recorded the depths up to 9 km in several areas along the 305 km length section. The data details can be found in the "Ocean_bed_data.xlsx file. In this file, L and x represent the length and width of the desired section of the ocean bed. Note that negative values in the excel file indicate depths as the depth is measured from the water surface to downwards to reach the desired location of the ocean bed. Q1(a) (3 marks) Import the data from the "Ocean_bed_data.xlsx" file. Make sure that all units are consistent. For six equally spaced locations along the 300 km long section, plot the corresponding depth vs width data in a 3-by-2 subplot configuration in figure (1). Plot the data using red circles and use the location (i.e., length, L = 0 m) information in the title for each subplot. Hint: Use a for loop to plot and use sprintf() to print the titles for each subplot. Q1(b) (4 marks) Use the composite trapezoidal rule to integrate the depth data of each cross section from L = 0 to 300 km to calculate the cross-sectional areas, X-area. Consider using only the positive values for X- area. Print the obtained X-area and corresponding location (3 decimal places) in a text file named "X- area.txt". The print format inside the file should look like following table Location (km) X-area (km2) 0 10 xxx.xxx 20 30 40 xxx.xxx xxx.xxx xxx.xxx xxx.xxx Hints: Use a function file to compute the composite trapezoidal rule for vectors. You might consider using the abs() function to take the absolute X-area values. Q1(c) (8 marks) (1) Plot the X-area against the location (length) data obtained in 01(b) with black diamonds in figure (2). Calculate the volume of the ocean bed stretching the length (L=0 to 300 km) using Simpson's 1/3rd rule. Print the result using fprintf(). Can you also calculate the volume using Simpson's 3/8th rule for this data set? Print your thoughts using another fprintf(). (i) During the installation phase, the project team noticed a rise in the ocean bed in the negative L direction due to the reduction of the cross-sectional area, X-area, which can be described by the following equation, 7 Xarea 10BL where L is the location. Fit the X-area and location data for the above-mentioned relationship. Plot this relationship using a suitable range of L value (i.e. from-305 km SLS 305 km) as a blue dashed line in the same figure (figure 2). (ii) Use any suitable root finding methods to determine the location for X-area = 50 km2. Use a red diamond to mark this location on the same figure. Print the root as an answer. Include legend for the figure in a suitable place so it does not overlap any part of the plots. Hints: you can use polyfit() function to fit the data and extract a and values. R 20 A B 1 L(km) x=0 km 2 0 3 10 4 5 5 30 6 6 40 7 2 50 8 60 9 70 10 80 11 90 12 100 13 110 14 120 15 130 16 140 17 150 18 160 19 170 20 180 20 21 190 22 200 23 210 24 220 25 230 26 240 27 250 28 260 29 270 30 280 31 290 32 300 33 34 30 D E F G H M N 0 P Q x=2 km x=4 km x=6 km x=8 km x=10 km x=12 km x=14 km x=16 km x=18 km x=20 km x=22 km x=24 km xx=26 km x=28 km x=30 km 0 -0.5217 -0.9014 -2.3757 -3.2554 -3.622 -4.0032 -4.1076 -3.9046 -3.4531 -2.6621 -2.6134 -2.333 -2.0669 -1.3831 0 0 -0.5029 -0.9187 -2.3652 -3.3126 -3.6862 -4.0404 -4.1878 -4.0343 -3.4693 -2.7238 -2.5695 -2.2925 -1.9783 -1.3931 0 0 -0.4447 -1.1522 -2.3649 -3.3313 -3.8602 -4.2124 -4.284 -4.0577 -3.5416 -2.876 -2.5783 -2.425 -2.0197 -1.4355 0 0 -0.5225 -1.164 -2.4265 -3.2947 -3.9821 -4.2985 -4.3443 -4.1669 -3.7049 -3.0532 -2.6052 -2.4249 -2.1053 -1.6096 0 0 0 -0.5791 -1.3011 -2.4182 -3.4595 -4.0444 -4.4179 -4.5012 -4.1767 -3.6849 -3.1539 -2.6324 -2.575 -2.2722 -1.5713 0 o 0 -0.7705 -1.232 -2.5061 -3.4411 -4.0858 -4.5009 -4.5595 -4.3362 -3.8603 -3.2111 -2.7478 -2.5583 -2.2897 -1.7119 0 0 -0.7821 -1.3868 -2.5511 -3.4176 -4.2079 -4.5796 -4.5433 -4.2912 -3.8762 -3.3085 -2.9113 -2.5404 -2.3199 -1.7038 0 0 -0.7769 -1.4156 -2.6 -3.482 -4.1295 -4.559 -4.5982 -4.5559 -3.8795 -3.2423 -2.8517 -2.646 -2.2713 -1.7829 0 0 -0.7578 -1.585 -2.766 -3.5281 -4.2027 -4.6351 -4.66 -4.5046 -4.0832 -3.2975 -2.9117 -2.7067 -2.4273 -1.8691 0 0 -0.9172 -1.6698 -2.701 -3.6639 -4.2848 -4.872 -4.8147 -4.7038 -4.0931 -3.5023 -3.0248 -2.8643 -2.5018 -1.7817 0 0 -0.911 -1.6931 -2.7539 -3.5818 -4.4444 -4.7744 -4.9645 -4.6724 -4.2191 -3.5828 -3.0682 -2.8321 -2.451 -1.9074 0 0 -1.0618 -1.8361 -2.7906 -3.7277 -4.5825 -4.9987 -5.0861 -4.8979 -4.2377 -3.6106 -3.1299 -2.8229 -2.4904 -1.91 0 0 0 -1.1079 -1.9323 -2.8909 -3.7534 -4.6046 -5.1719 -5.284 -5.1027 -4.3143 -3.7875 -3.0682 -2.8256 -2.5462 -2.1258 0 0 -1.1402 -1.9313 -2.8584 -3.8299 -4.6538 -5.3276 -5.3639 -5.297 -4.4078 -3.8585 -3.1229 -2.9736 -2.6424 -2.1522 0 0 -1.0617 -2.1047 -2.9574 -3.9444 -4.8448 -5.4721 -5.6436 -5.2955 -4.4991 -3.9309 -3.2436 -3.0081 -2.6493 -2.175 0 0 -1.1482 -2.1181 -3.144 -3.9946 -4.8121 -5.7739 -5.8045 -5.6247 -4.5456 -4.0121 -3.3222 -2.9706 -2.7381 -2.1694 0 0 -1.1775 -2.157 -3.1861 -4.0285 -4.9793 -5.9471 -5.9941 -5.782 -4.6452 -4.035 -3.3786 -3.0938 -2.8056 -2.1545 0 0 -1.3622 -2.333 -3.0612 -4.0691 -4.9431 -6.0897 -6.0091 -5.8245 -4.7977 -4.1216 -3.291 -3.2649 -2.8272 -2.3471 0 0 0 -1.409 -2.4019 -3.2534 -4.089 -5.0888 -6.2336 -6.1921 -6.0205 -4.859 -4.2295 -3.4348 -3.2255 -2.8249 -2.3861 0 0 -1.3302 -2.3599 -3.3075 -4.2145 -5.1061 -6.4486 -6.4547 -6.1734 -4.9283 -4.3226 -3.4039 -3.197 -3.0491 -2.4782 0 0 0 -1.4662 -2.535 -3.251 -4.2993 -5.2723 -6.5395 -6.5853 -6.3911 -5.0043 -4.4035 -3.5482 -3.3739 -3.0795 -2.4799 0 o 0 -1.4502 -2.54845 -3.37415 -4.372 -5.3538 -6.71895 -6.8081 -6.56555 -5.0696 -4.504 -3.60465 -3.33995 -3.19045 -2.54545 0 0 -1.47352 -2.60485 -3.4365 -4.45361 -5.45429 -6.87539 -7.00722 -6.75082 -5.13851 -4.59788 -3.67872 -3.3698 -3.28856 -2.5945 0 0 -1.49684 -2.66125 -3.49885 -4.53522 -5.55478 -7.03183 -7.20634 -6.93609 -5.20742 -4.69176 -3.75279 -3.39965 -3.38667 -2.64355 0 0 -1.52016 -2.71765 -3.5612 -4.61683 -5.65527 -7.18827 -7.40546 -7.12136 -5.27633 -4.78564 -3.82686 -3.4295 -3.48478 -2.6926 0 0 -1.54348 -2.77405 -3.62355 -4.69844 -5.75576 -7.34471 -7.60458 -7.30663 -5.34524 -4.87952 -3.90093 -3.45935 -3.58289 -2.74165 0 0 -1.5668 -2.83045 -3.6859 -4.78005 -5.85625 -7.50115 -7.8037 -7.4919 -5.41415 -4.9734 -3.975 -3.4892 -3.681 -2.7907 0 0 -1.59012 -2.88685 -3.74825 -4.86166 -5.95674 -7.65759 -8.00282 -7.67717 -5.48306 -5.06728 -4.04907 -3.51905 -3.77911 -2.83975 0 0 0 -1.61344 -2.94325 -3.8106 -4.94327 -6.05723 -7.81403 -8.20194 -7.86244 -5.55197 -5.16116 -4.12314 -3.5489 -3.87722 -2.8888 0 0 -1.63676 -2.99965 -3.87295 -5.02488 -6.15772 -7.97047 -8.40106 -8.04771 -5.62088 -5.25504 -4.19721 -3.57875 -3.97533 -2.93785 0 0 0 -1.66008 -3.05605 -3.9353 -5.10649 -6.25821 -8.12691 -8.60018 -8.23298 -5.68979 -5.34892 -4.27128 -3.6086 -4.07344 -2.9869 0