Please solve (d) and (e) parts

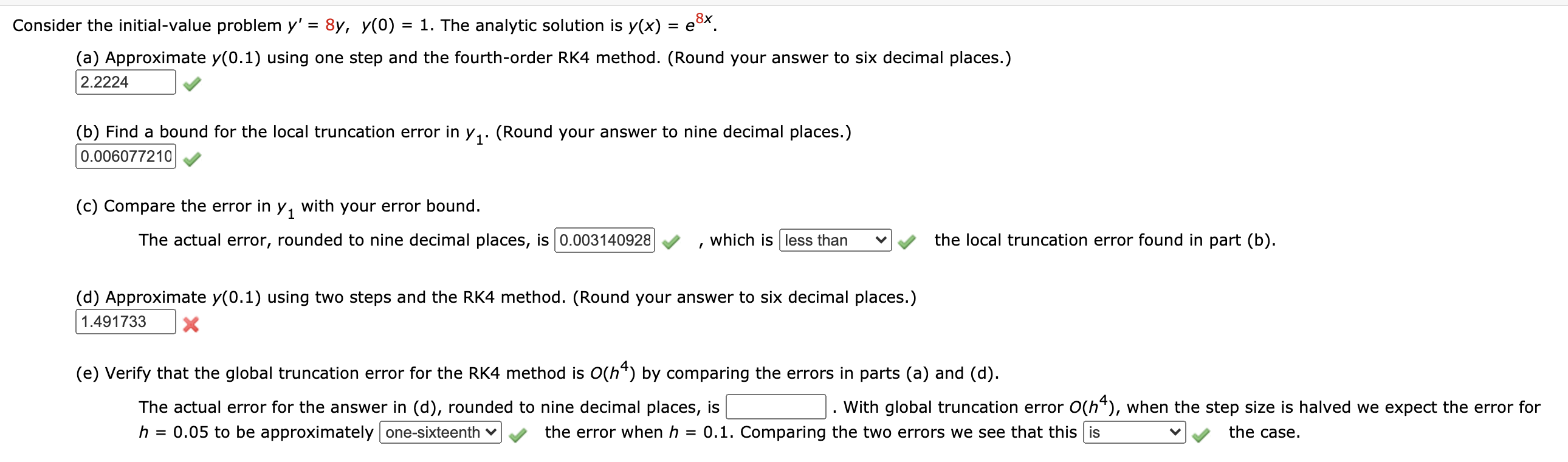
Consider the initial-value problem y' = 8y, y(0) = 1. The analytic solution is y(x) = es". (a) Approximate y(0.1) using one step and the fourth-order RK4 method. (Round your answer to six decimal places.) 2.2224 (b) Find a bound for the local truncation error in yl. (Round your answer to nine decimal places.) 0.006077210 V (c) Compare the error in y1 with your error bound. The actual error, rounded to nine decimal places, is 0.003140928 , which is less than v y the local truncation error found in part (b). (d) Approximate y(0.1) using two steps and the RK4 method. (Round your answer to six decimal places.) 1.491733 x (e) Verify that the global truncation error for the RK4 method is 0(h4) by comparing the errors in parts (a) and (d). The actual error for the answer in (d), rounded to nine decimal places, is . With global truncation error 0(h4), when the step size is halved we expect the error for h = 0.05 to be approximately one-sixteenth v the error when h = 0.1. Comparing the two errors we see that this is v the case