please solve on page only part b

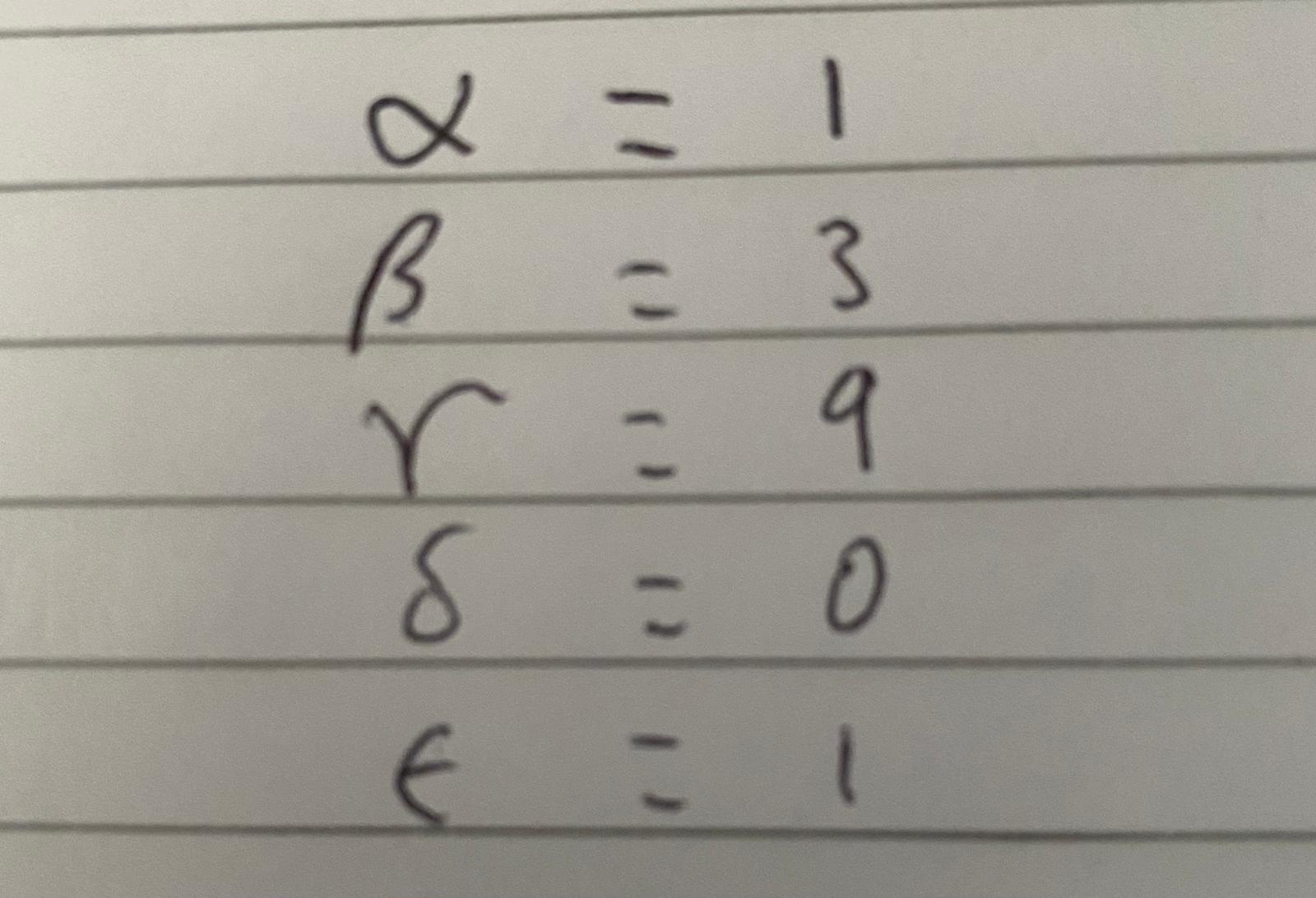
4. In this question any Greek letters a, ,8, '7, 6, 6 refer to the digits of your student number, as described in the instructions on the second page of the exam. a. Let B, be a Brownian motion. Consider a stochastic process X, given by X: = (2 + E)Btl+7 + tl-E-aBt Using Ito's lemma, work out a stochastic differential equation satised by the process. [5 marks] b. Assume that the interest rate is zero. A European call option on a stock with strike price 1 + a + 6 and maturity date a year from now has price 1 + ,8. A European put option on the same stock, with the same strike price and maturity, has price 1 + E. If these prices are arbitrage free, what is the current price of the stock? [5 marks] c. Suppose that there is a forward contract with a delivery price of K 2 30 + (1 + 70/2 on a stock with a current price of 25 + (1 + 10/2. Suppose that the maturity date is one year from now, and that the annual interest rate is extremely high, with value 7' = (1/ 2) + (04/ 20). Assume that it costs nothing to enter the forward contract in either the long or short position. Starting from no wealth, explain how to make an arbitrage prot by detailing which position you would take on the forward contract, and what transactions you would make at what times. [6 marks] d. Consider the stochastic process K = (1 + '03; + (1 + 6)(B,2 t), where B, is a Brownian motion. Show that it is a Martingale. [4 marks] \f