Question: Please solve the following modular operations. 113 (mod 7) = Enter the prime factorisation (in exponent form) of 600. Using the information above, enter

prime factorisation (in exponent form) of 600. Using the information above, enter

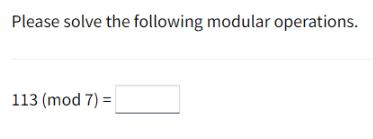
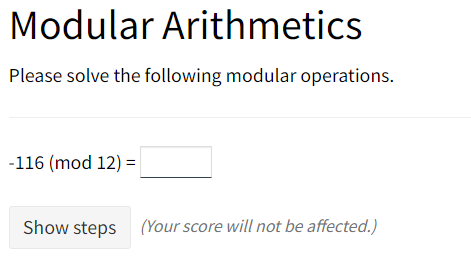
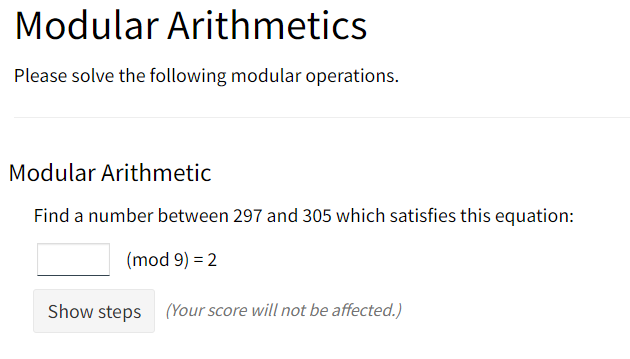
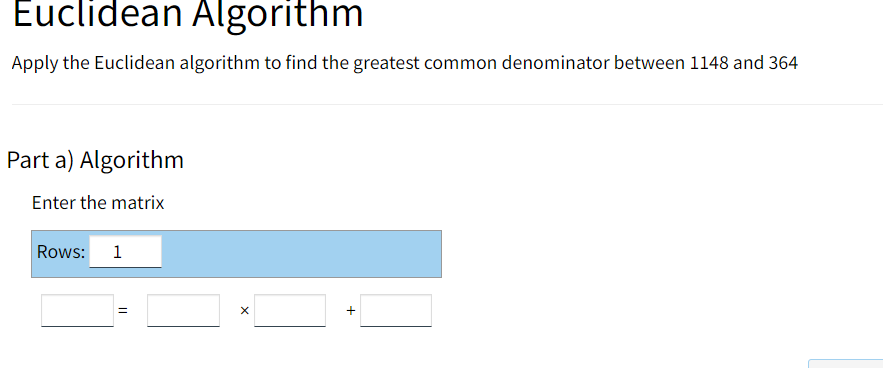
Please solve the following modular operations. 113 (mod 7) = Enter the prime factorisation (in exponent form) of 600. Using the information above, enter the gcd and the lcm of 600 and 13125. gcd (600,13125)= Icm (600,13125) = Show steps (You will lose 1 mark.) Convert 5454 from base 9 to base 10. 54549 = 10 Modular Arithmetics Please solve the following modular operations. -116 (mod 12) = Show steps (Your score will not be affected.) Modular Arithmetics Please solve the following modular operations. Modular Arithmetic Find a number between 297 and 305 which satisfies this equation: (mod 9) = 2 Show steps (Your score will not be affected.) Modular Arithmetics Please solve the following modular operations. Modular Arithmetic Find a number which satisfies this equation: 98 (mod )=3 Euclidean Algorithm Apply the Euclidean algorithm to find the greatest common denominator between 1148 and 364 Part a) Algorithm Enter the matrix Rows: 1 + Part b) gcd gcd (1148,364)= Part c) LCM Lowest Common Multiple Use the information above to calculate the lowest common multiple between 1148 and 364. Icm(1148,364)= Show steps (You will lose 1 mark.) Answer: Submit all parts Unanswered Submit part Unanswered Submit part Unanswered

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

Case of Brian B. and the Medical File Brian B. is taken into an exam room in the office of Dr. K. by the medical assistant, Amy. Amy gets into an animated discussion with Brian about their mutually...

Exercise 5.18 Revaluation model On 1 July 2022, Resonante Ltd acquired two assets within the same class of plant and equipment. Information these assets is as follows Cost Expected useful life...

What are the differences between safety hazards and health hazards? If you were the HR manager for a chain of restaurants and bars based in Texas, what safety and/or health precautions should be...

content/1191485/viewContent/6000337/View Module assessment > NUMBAS Modular Arithmetics Please solve the following modular operations. Number Theory (Core) Modular Arithmetic Modular Arithmetic...

\f\fessment AdviceModular Arithmetics Please solve the following modular operations. Expected answer 2 317 (mod 9)\fJon Score TON Part b) god Score. DUH god(1378 125 Expected answer 19 Part c) LCM...

1. Discuss what type of title each party has and how it can be lawfully transferred. 2. Who do you think the court should choose as the rightful owner and why? 3. Why do you think the car was...

South Western Railway's (SWR) franchise that commenced in August '17 included two major timetable change commitments. (Documents relating to all franchise agreements can be accessed from the DfT...

This question is related to Crytograpy. please the answer the question properly. (1 point) Solve the following modular equations. In each case please use the smallest positive solution. a) 7+2=6 mod...

(1 point) Compute the following modular exponents. 134 mod 15 = 23 mod 5 = 35 mod 8 = (1 point) Solve the following modular equations. In each case please use the smallest positive solution. a) 14 +...

Find two other examples of online pricing mistakes. How did the companies handle the problems resulting from the pricing errors? The Internet is great for selling products and services. But dont make...

What is the connection between customer service and employee empowerment? Is employee empowerment always a good idea? Why or why not?

Daniel Burrows, the founder of TruckLabs, initially established manufacturing operations in Asia to minimize costs. However, he chose to keep critical functions such as software development,...

Simkin Corporation purchased land for $420,000. Later in the year, the company sold a different piece of land with a book value of $155,000 for $110,000. How are the effects of these transactions...

What are the basic classifications found on an income statement for a merchandising business as compared to a service business?

The Regal Cycle Company manufactures three types of bicycles-a dirt bike, a mountain bike, and a racing bike. Data on sales and expenses for the past quarter follow: Management is concerned about the...

Calculating Project NPV you have been hired as a consultant for Pristine Urban-Tech Zither, Inc. (PUTZ), manufacturers of fine zithers. The market for, zithers is growing quickly. The company bought...

Sheaves Corporation economists estimate that a good business environment and a bad business environment are equally likely for the coming year. The managers of Sheaves must choose between two...

Which of the following advertising mediums has experienced a meteoric rise in the last couple of decades? Television Instagram Influencer marketing The internet

Show that if 2n 1 is prime, then n is prime.

Prove that n2 + 1 2n when n is a positive integer with 1 n 4.

List all 3-permutations of {1, 2, 3, 4, 5}. The remaining exercises in this section develop another algorithm for generating the permutations of {1, 2, 3, . . . , n}. This algorithm is based on...

Research by Elizabeth Loftus shows that eyewitness recognition is very prone to what psychologists call a. a flashbulb memory. b. automatic encoding. c. a false positive. d. a recency effect.

Identify some methods that people use to solve problems and make decisions.

Compare and contrast some methods of measuring intelligence.