Please solve the problems in the attachment. Thank you!!

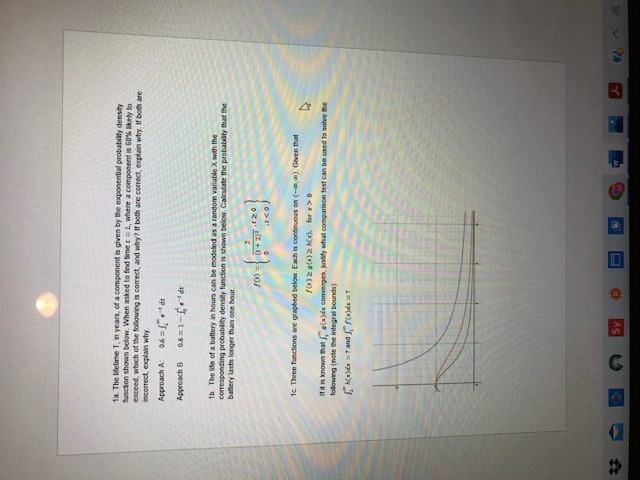
In The lifetime T. in years, of a component is given by the exponential probability density function shown below. When asked to find time : = L, where a component is 5075 bely to exceed which of the following is correct, and why? If both are correct, explain why. If both are incorrect, explain why. Approach A: as = ) . * di Approach B 0.6 =1 -[ d 1b, The life of a battery in hours can be modeled as a random variable X with the con cspending probability density function is shown below Calculate the probability that free battery lasts longer than one hour. 10 = 0+3 .120 1c Three functions are graphed below Each is continuous on (-as, a). Given that if it is known that J, etalds converges, justify what comparison test can be used to solve the following (note the integral bounds) Holds = and [, /tajds = Sy