please solve these problems, will be really appreciated, take your time and solve please, its important

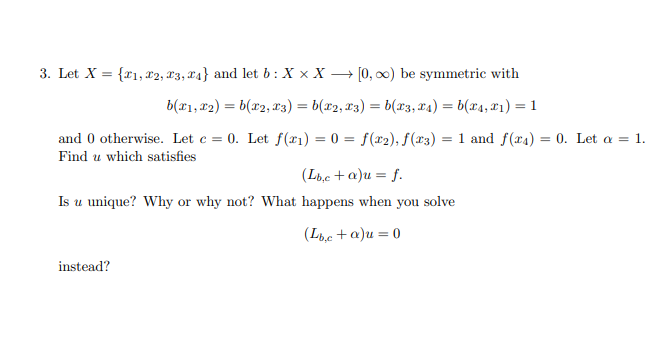
1. Let X = {x1, 12, 13, x4} and let b : X x X - [0, co) be symmetric with b(21, 12) = 3, b(12, 13) = 1, b(x2, 14) = 2. Let c = 0 and let m(x) = deg(x). Let f. ge C(X) be functions defined by f(x1) = 1, f(x2) = 2, f(x3) = 3, f(x4) = 4, and g(21) = 0, g(x2) = -3, 9(23) = 4, 9(x4) = -1. (a) Calculate the inner product (f, g), and norms |If| | and ||g| in 62(X, m). (b) Find IIf - gl. (c) Show that (|h]| = 0 for a function he C(X) if and only if h = 0. (d) Calculate Qu,c(f, 9), Qu,c(f) and Qb,c(g). (e) Find Lbemf(x) and Lb,e,mg(x) for re X. (f) Show that Qo,c(f, 9) = (Lbe,mf.9) = (f, Lbe,mg). (g) Identify the maximum and minimum of both f and g. Verify that Lbcmf (2) 2 0 at the maximum and Lbemf(x) [0, co) be symmetric with b(1, 12) = b(12, 13) = 1 and 0 otherwise. Let c(x1) = 1 and c(r2) = c(x3) = 0. Let f(x1) =1 = f(x3) and f(x2) =0. Find u which satisfies Lb,cut = f. Is u unique? Why or why not? What happens if c =0 in the above?3. Let X = {x1, x2, x3, } and let b : X x X -> [0, co) be symmetric with b(x1, 12) = b(x2, x3) = b(12, 13) = b(x3, TA) = b(x4, r]) = 1 and 0 otherwise. Let c = 0. Let f(21) = 0 = f(x2), f(x3) = 1 and f(x4) = 0. Let a = 1. Find u which satisfies ( Lbe ta)u = f. Is u unique? Why or why not? What happens when you solve (Lbe to)u = 0 instead