Please solve this coding problem (python & sagemath)

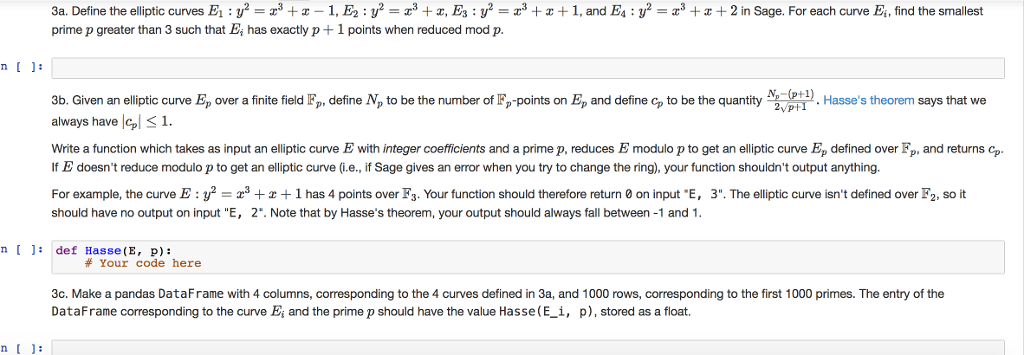
3a. Define the elliptic curves El : z + z-1, E2 : y-z? + z E3 : 3,2 prime p greater than 3 such that Ei has exactly p+1 points when reduced mod p z? + z + 1, and Ei : y2-x3 +x + 2 n Sage. For each curve E, find the smallest b. Given an ellitic curve Ep over a finite field F define N, to be the number of F,-points on E, and define c to be the quantityasse's theorem says that we always have lo1. Write a function which takes as input an elliptic curve E with integer coefficients and a prime p, reduces E modulo p to get an elliptic curve Ep defined over Fp, and returns cp f E doesn't reduce modulo p to get an elliptic curve (i.e., if Sage gives an error when you try to change the ring), your function shouldn't output anything. For example, the curve : r' + z + 1 has 4 points over 3 Your function should therefore return on input ee, 3 The elliptic curve isnt defined over F2 so it should have no output on input "E, 2". Note that by Hasse's theorem, your output should always fall between -1 and 1 n [ : def Hasse (E, p): # Your code here 3c. Make a pandas DataFrame with 4 columns, corresponding to the 4 curves defined in 3a, and 1000 rows, corresponding to the first 1000 primes. The entry of the DataFrame corresponding to the curve E and the prime p should have the value Hasse(E_i, p), stored as a float. 3a. Define the elliptic curves El : z + z-1, E2 : y-z? + z E3 : 3,2 prime p greater than 3 such that Ei has exactly p+1 points when reduced mod p z? + z + 1, and Ei : y2-x3 +x + 2 n Sage. For each curve E, find the smallest b. Given an ellitic curve Ep over a finite field F define N, to be the number of F,-points on E, and define c to be the quantityasse's theorem says that we always have lo1. Write a function which takes as input an elliptic curve E with integer coefficients and a prime p, reduces E modulo p to get an elliptic curve Ep defined over Fp, and returns cp f E doesn't reduce modulo p to get an elliptic curve (i.e., if Sage gives an error when you try to change the ring), your function shouldn't output anything. For example, the curve : r' + z + 1 has 4 points over 3 Your function should therefore return on input ee, 3 The elliptic curve isnt defined over F2 so it should have no output on input "E, 2". Note that by Hasse's theorem, your output should always fall between -1 and 1 n [ : def Hasse (E, p): # Your code here 3c. Make a pandas DataFrame with 4 columns, corresponding to the 4 curves defined in 3a, and 1000 rows, corresponding to the first 1000 primes. The entry of the DataFrame corresponding to the curve E and the prime p should have the value Hasse(E_i, p), stored as a float