Please solve this problem using Matlab.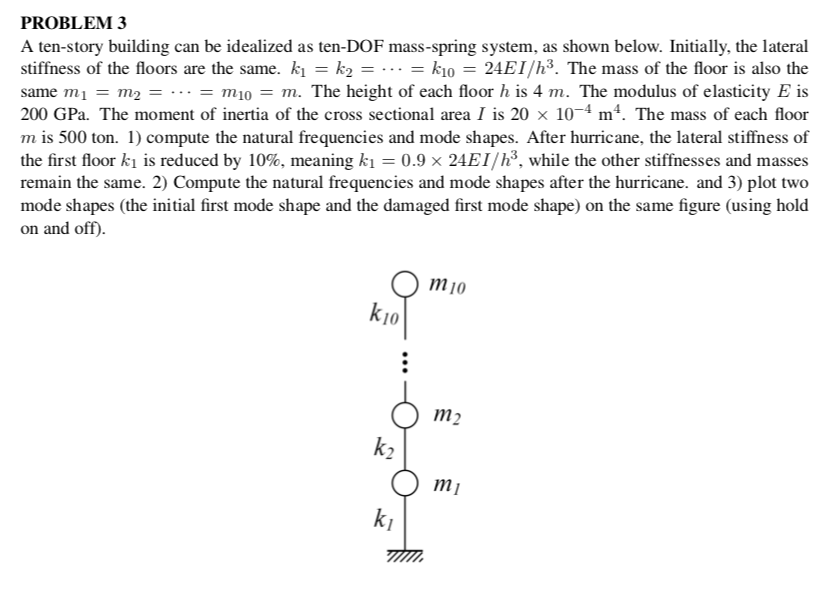

PROBLEM 3 A ten-story building can be idealized as ten-DOF mass-spring system, as shown below. Initially, the lateral stiffness of the floors are the same. kk2k10 24EI/h3. The mass of the floor is also the same mim2mi0m. The height of each floor h is 4 m. The modulus of elasticity E is 200 GPa. The moment of inertia of the cross sectional area 1 is 20 10-4 m. The mass of each floor m is 500 ton. 1 compute the natural frequencies and mode shapes. After hurricane, the lateral stiffness of the first floor ki is reduced by 10%, meaning ki = 0.9 x 24E1/h3, while the other stiffnesses and masses remain the same. 2) Compute the natural frequencies and mode shapes after the hurricane. and 3) plot two mode shapes (the initial first mode shape and the damaged first mode shape) on the same figure (using hold on and off) m10 10 m2 k2 O mi ki PROBLEM 3 A ten-story building can be idealized as ten-DOF mass-spring system, as shown below. Initially, the lateral stiffness of the floors are the same. kk2k10 24EI/h3. The mass of the floor is also the same mim2mi0m. The height of each floor h is 4 m. The modulus of elasticity E is 200 GPa. The moment of inertia of the cross sectional area 1 is 20 10-4 m. The mass of each floor m is 500 ton. 1 compute the natural frequencies and mode shapes. After hurricane, the lateral stiffness of the first floor ki is reduced by 10%, meaning ki = 0.9 x 24E1/h3, while the other stiffnesses and masses remain the same. 2) Compute the natural frequencies and mode shapes after the hurricane. and 3) plot two mode shapes (the initial first mode shape and the damaged first mode shape) on the same figure (using hold on and off) m10 10 m2 k2 O mi ki