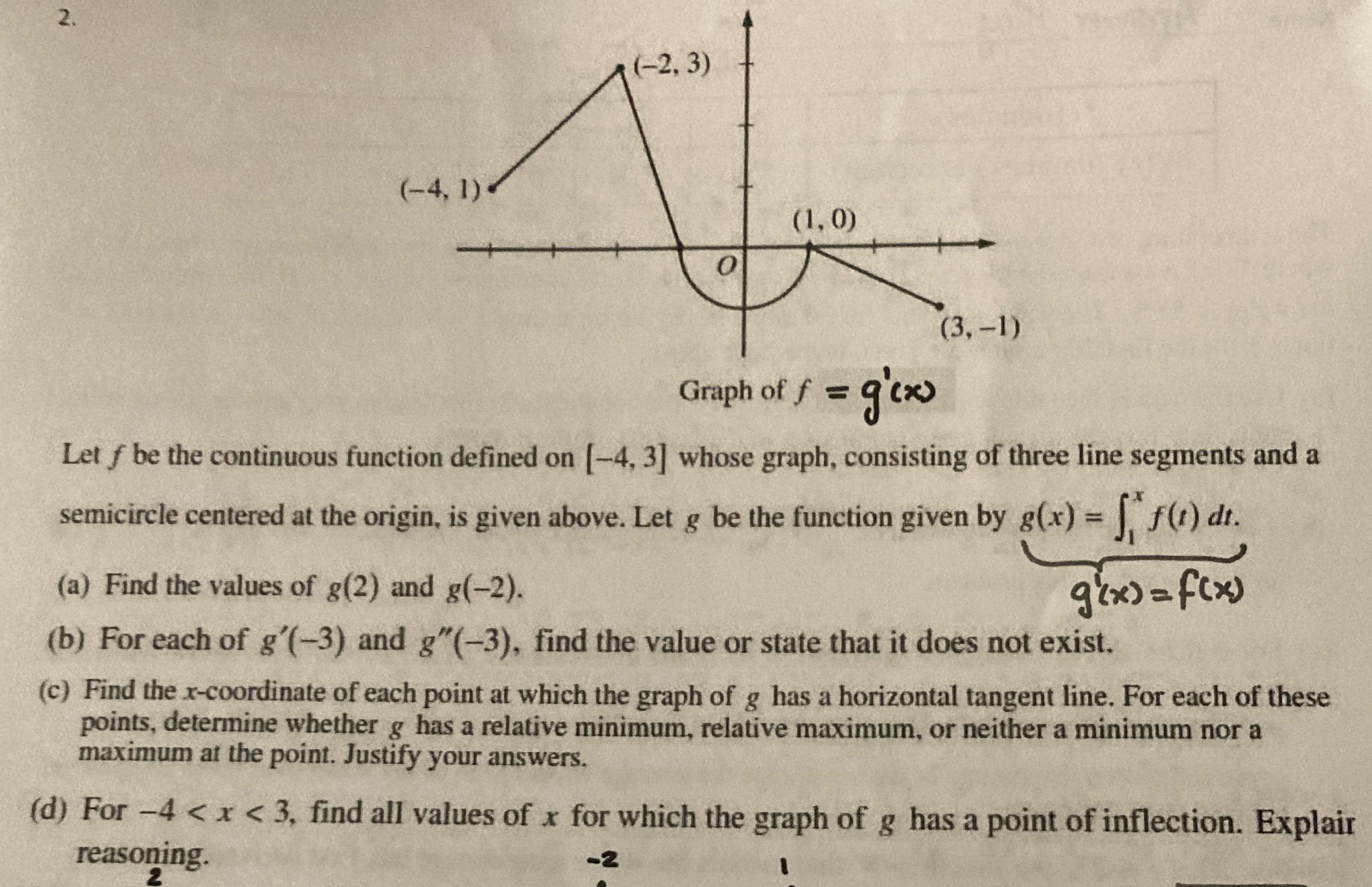
Please solve this question by changing g'(x) to g"(x).

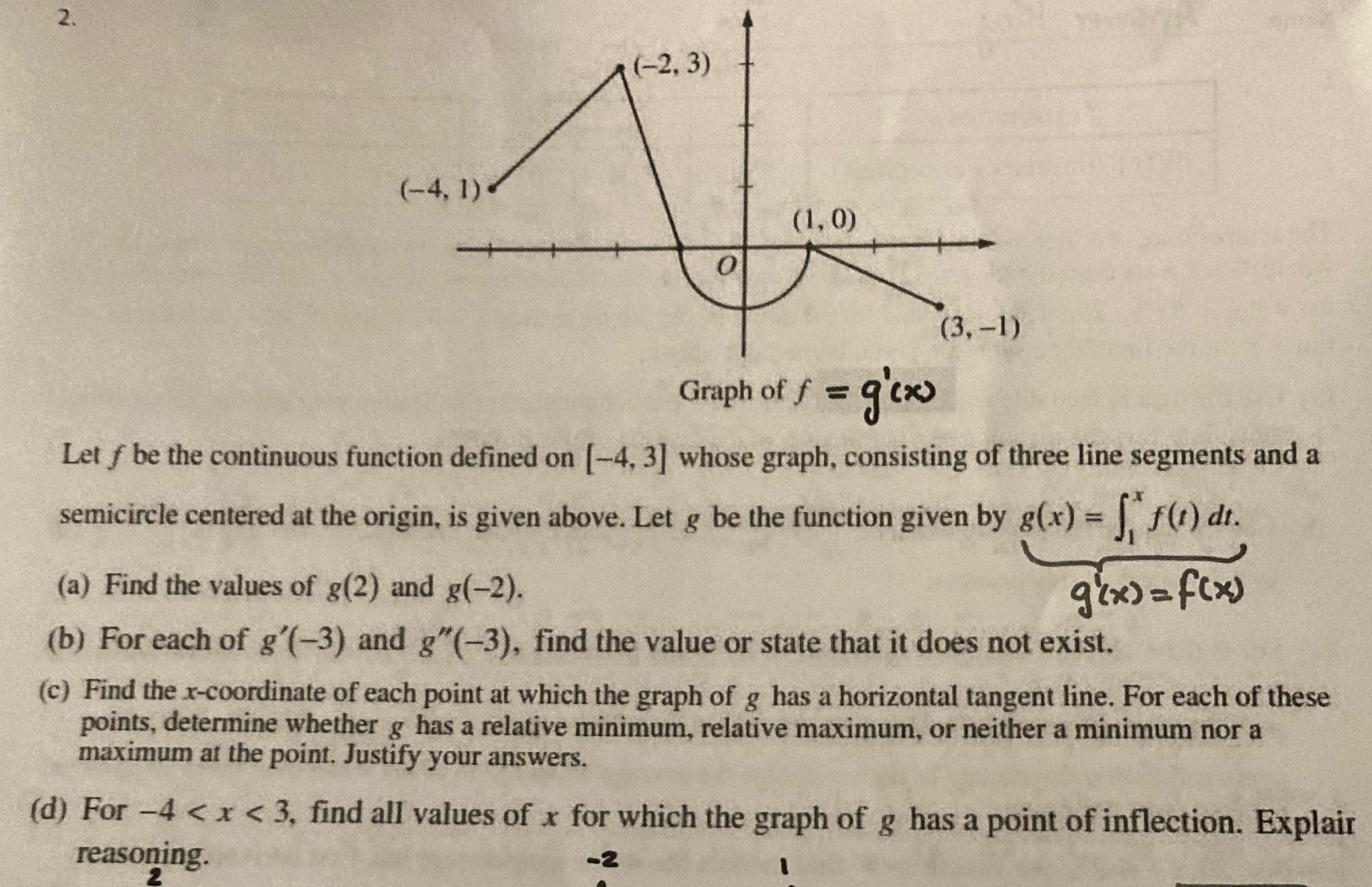
(-2. 3) (-4, 1) - (1, 0) O (3,-1) Graph of f = 9 (x) Let f be the continuous function defined on [-4, 3] whose graph, consisting of three line segments and a semicircle centered at the origin, is given above. Let g be the function given by g(x) = [, F(r) di. (a) Find the values of g(2) and g(-2). g (x) = f(x) (b) For each of g'(-3) and g"(-3), find the value or state that it does not exist. (c) Find the x-coordinate of each point at which the graph of g has a horizontal tangent line. For each of these points, determine whether g has a relative minimum, relative maximum, or neither a minimum nor a maximum at the point. Justify your answers. (d) For -4